Vector Calculus Of The Turbine Design In Real Life Applications Presentation

Introduction to Vector Calculus in Turbine Design
Vector calculus plays a crucial role in the design and optimization of turbines in real-life applications. Turbine designers use vector calculus to analyze and manipulate vectors and vector fields, enabling them to understand and improve turbine performance. Understanding vector calculus is essential for optimizing turbine efficiency, power output, and overall design.	Image Source
		1

Basics of Vector Calculus
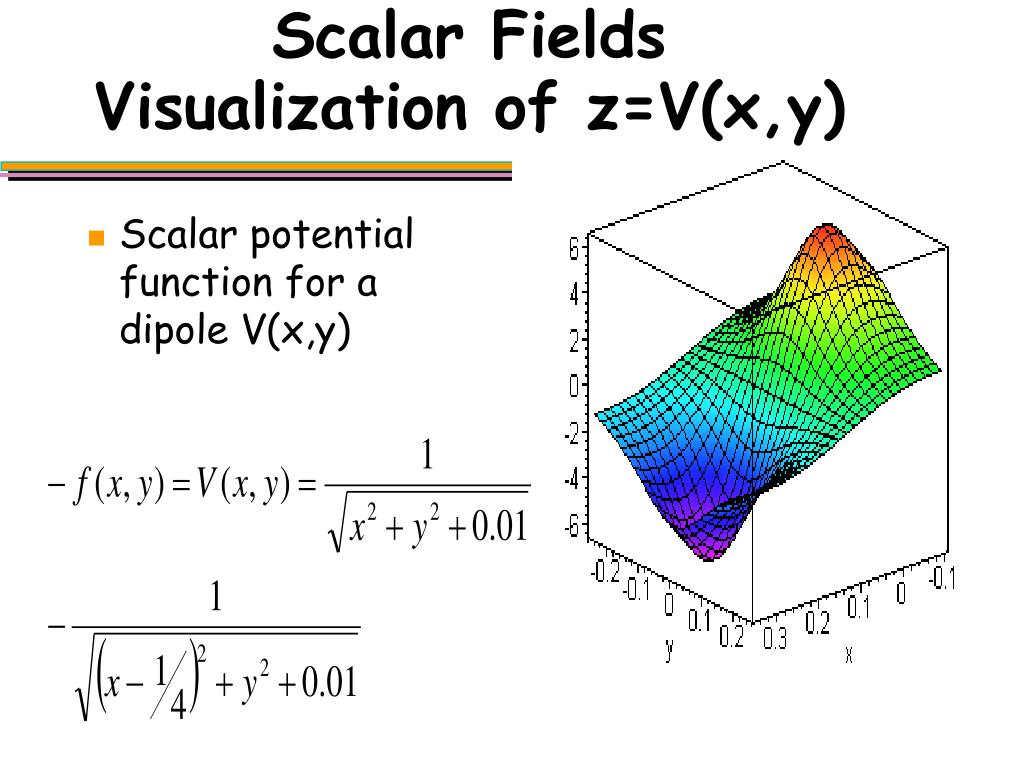
Vector calculus involves the study of vector fields, which are functions that assign a vector to every point in space. Key concepts in vector calculus include gradient, divergence, and curl. The gradient of a scalar function represents the direction and magnitude of the steepest ascent, aiding in turbine design optimization.	Image Source
		2

Vector Calculus and Turbine Efficiency
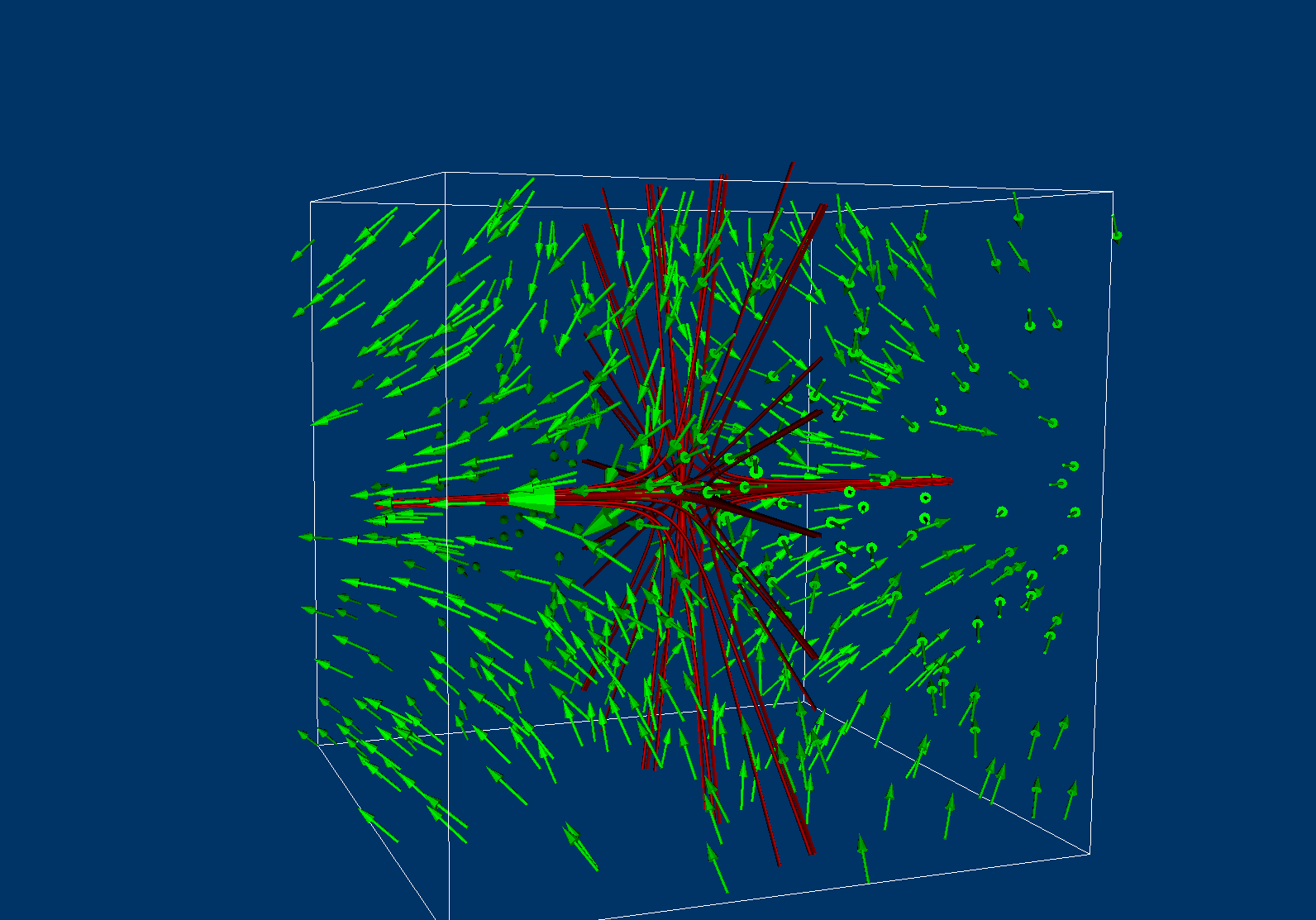
Vector calculus helps in optimizing turbine efficiency by analyzing and manipulating fluid flow vectors within the turbine. By using the divergence operator, designers can identify regions of high or low fluid density, helping to minimize energy losses and maximize turbine performance. The curl operator helps in understanding the rotation and vorticity of fluid flow, aiding in the design of efficient turbine blades.	Image Source
		3

Turbine Design and Vector Field Visualization
Visualizing vector fields using techniques like streamlines and vector plots helps turbine designers gain insights into fluid flow patterns. Streamlines provide a visual representation of the fluid flow path, aiding in identifying areas of recirculation or turbulence. Vector plots display the magnitude and direction of the fluid velocity, assisting designers in optimizing blade shape and angle.	Image Source
		4

Numerical Simulations and Vector Calculus
Numerical simulations based on vector calculus principles allow designers to analyze complex fluid flow phenomena within turbines. Finite element methods and computational fluid dynamics (CFD) utilize vector calculus to solve fluid flow equations and simulate turbine performance. These simulations help designers understand the impact of various design parameters on turbine efficiency and optimize turbine performance.	Image Source
		5

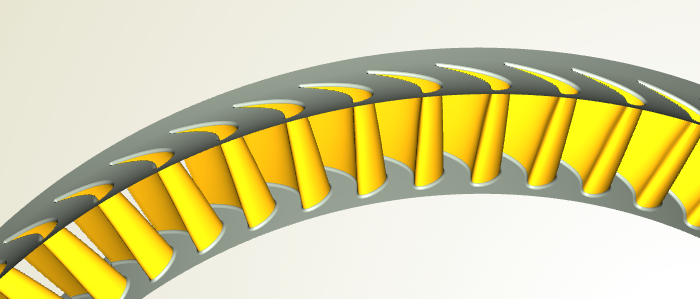
Vector Calculus and Turbine Blade Design
Vector calculus plays a crucial role in turbine blade design by optimizing blade shape and angle to maximize energy conversion. The gradient operator aids in determining the steepest ascent of fluid flow along the turbine blade, optimizing power output. The curl operator helps in designing blade profiles that minimize turbulence and maximize energy extraction from the fluid flow.	Image Source
		6

Vector Calculus and Turbine Control Systems
Vector calculus is also essential in turbine control systems, which regulate turbine operation based on real-time data. By analyzing fluid flow vectors, control systems can adjust turbine parameters such as blade pitch or rotor speed to optimize performance. Vector calculus enables control systems to react to changes in fluid flow conditions and maintain optimal turbine operation.	Image Source
		7

Real-Life Applications of Vector Calculus in Turbine Design
Vector calculus is applied in various real-life turbine design applications, including wind turbines, hydroelectric turbines, and gas turbines. In wind turbines, vector calculus helps optimize blade angle and shape to maximize power generation from wind flow. In hydroelectric turbines, vector calculus aids in designing efficient water flow patterns to generate maximum electricity.	Image Source
		8

Conclusion
Vector calculus is a powerful tool in the design and optimization of turbines in real-life applications. It enables designers to analyze and manipulate fluid flow vectors, optimize turbine efficiency, and maximize power output. Understanding vector calculus is crucial for engineers and designers working in the field of turbine design.	Image Source
		9

References (download PPTX file for details)
Insert relevant references and sources used i... Your second bullet... Your third bullet...
		10

Join the SlideMake Community