Physical Significance Of Wave Functions Presentation

Introduction to Wave Functions
The wave function is a mathematical description of a physical system in quantum mechanics. It contains information about the probability distribution of a particle's position or momentum. The square of the wave function (|Ψ|^2) gives the probability density of finding the particle at a particular location.	Image Source
		1

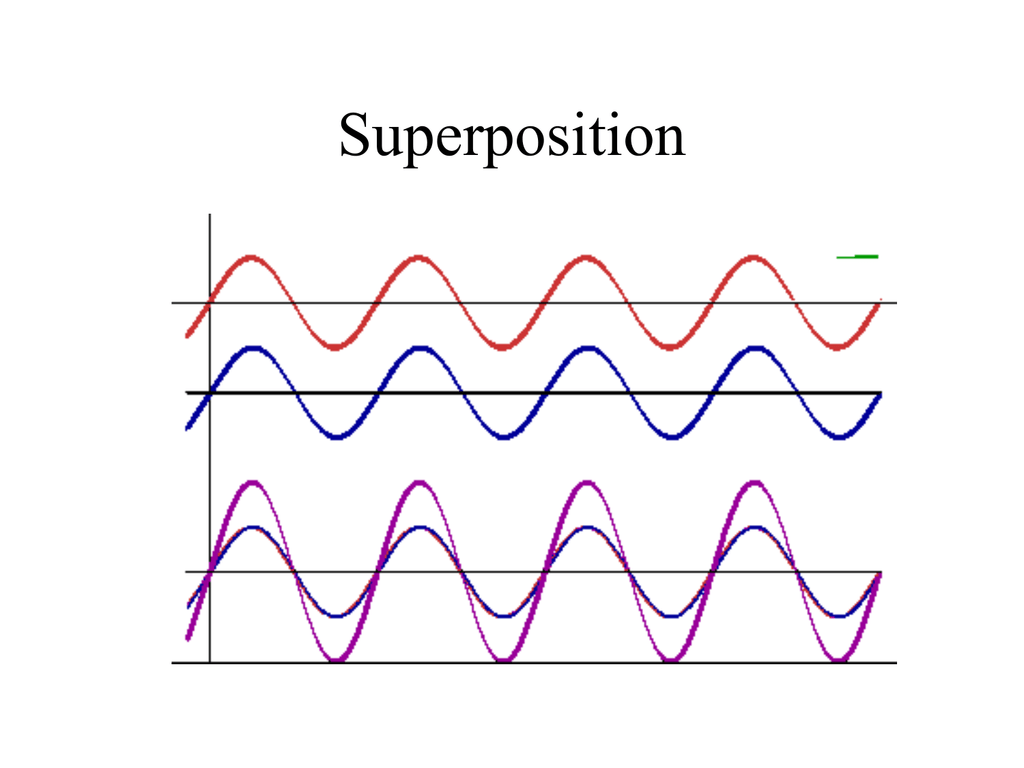
Wave Functions and Superposition
Wave functions can be combined through superposition, resulting in interference effects. This allows for the description of phenomena like diffraction and interference in wave-particle duality. Superposition of wave functions enables the representation of multiple possible states of a system simultaneously.	Image Source
		2

Wave Functions and Energy
Wave functions are solutions to the Schrödinger equation, which describes the behavior of quantum systems. The energy of a system can be determined from the wave function through the Hamiltonian operator. Eigenstates of the Hamiltonian operator correspond to specific energy levels of the system.	Image Source
		3

Wave Functions and Observables
Wave functions are used to calculate expectation values of observables like position, momentum, and energy. The expectation value is the average value that would be obtained if the measurement is repeated many times. These calculations provide insight into the physical properties and behavior of quantum systems.	Image Source
		4

Wave Functions and Uncertainty Principle
The uncertainty principle states that there is a fundamental limit to the precision with which certain pairs of physical properties can be known. Wave functions reflect the inherent uncertainty in position and momentum measurements of quantum particles. The spread of the wave function determines the uncertainty in the corresponding observable.	Image Source
		5

Conclusion
Wave functions have physical significance as they describe the probabilistic nature of quantum systems. They allow for the calculation of observables and provide insight into the behavior of particles. Wave functions are fundamental to understanding the wave-particle duality and the principles of quantum mechanics.	Image Source
		6

Join the SlideMake Community