Mc Nemar Test Presentation
| Introduction to McNemar Test | ||
|---|---|---|
| The McNemar Test is a statistical test used to analyze paired nominal data. It is named after the statistician Quinn McNemar who developed the test in 1947. The test is commonly used in medical and social sciences research. | ||
| 1 | ||
| Purpose of McNemar Test | ||
|---|---|---|
| The McNemar Test is used to determine if there is a significant difference in frequencies between two related groups or conditions. It is often used when analyzing data before and after an intervention or treatment. The test helps to assess whether the intervention had a significant effect. | ||
| 2 | ||
| Assumptions of McNemar Test | ||
|---|---|---|
| The data should be collected from a matched-pairs design, where each subject is measured twice under different conditions. The two conditions being compared should be mutually exclusive, meaning each subject can only belong to one condition. The dependent variable should be categorical or nominal, with two possible outcomes. | ||
| 3 | ||
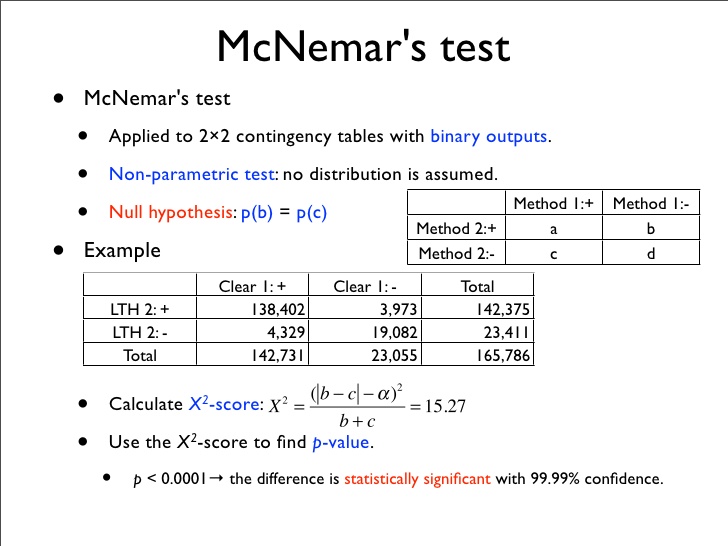
| Calculation of McNemar Test | ||
|---|---|---|
| The test uses a 2x2 contingency table to compare the frequencies of the two conditions. The table includes four cells: a, b, c, and d. The formula for calculating the McNemar statistic is (b - c)^2 / (b + c). |  | |
| 4 | ||
| Interpreting McNemar Test Results | ||
|---|---|---|
| The McNemar statistic follows a chi-square distribution with 1 degree of freedom. The obtained chi-square value is compared to the critical value to determine if there is a significant difference. If the obtained value is greater than the critical value, it indicates a significant difference between the conditions. | ||
| 5 | ||
| Advantages of McNemar Test | ||
|---|---|---|
| The McNemar Test is suitable for small sample sizes. It is a non-parametric test and does not assume a normal distribution. The test is easy to calculate and interpret, making it widely applicable in various fields. | ||
| 6 | ||
| Limitations of McNemar Test | ||
|---|---|---|
| The test assumes that the errors made in the two conditions are equal, which may not always be the case. It is sensitive to the assumption of independence between the paired observations. McNemar Test does not provide information about the direction of the difference, only whether a significant difference exists. | ||
| 7 | ||
| McNemar Test vs. Chi-Square Test | ||
|---|---|---|
| The McNemar Test is specifically designed for paired nominal data, while the chi-square test can analyze any categorical data. McNemar Test focuses on the difference between two conditions, while the chi-square test examines the association between variables. McNemar Test has higher statistical power when analyzing matched-pairs data. | ||
| 8 | ||
| Examples of McNemar Test Application | ||
|---|---|---|
| Analyzing changes in smoking habits before and after a smoking cessation program. Evaluating the effectiveness of a new medication by comparing symptoms before and after treatment. Assessing the impact of an educational intervention on student performance by comparing pre- and post-test scores. | ||
| 9 | ||
| Conclusion | ||
|---|---|---|
| The McNemar Test is a valuable statistical tool for analyzing paired nominal data. It helps researchers determine if there is a significant difference between two conditions. Understanding the assumptions, calculations, and interpretation of the test is crucial for accurate analysis and drawing valid conclusions. | ||
| 10 | ||
| References (download PPTX file for details) | ||
|---|---|---|
| McNemar, Q. (1947). Note on the sampling erro... Agresti, A. (2002). Categorical data analysis... Your third bullet... |  | |
| 11 | ||