Fractions,types Of Fractions Presentation

Introduction to Fractions
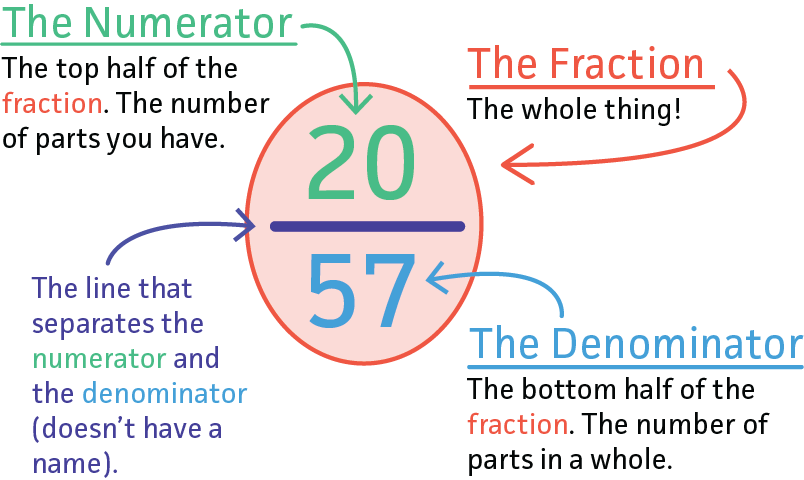
A fraction represents a part of a whole or a group. Numerator: The number on top of the fraction, representing the part. Denominator: The number on the bottom of the fraction, representing the whole.	Image Source
		1

Proper Fractions
Proper fractions have a numerator that is less than the denominator. The value of a proper fraction is always less than 1. Example: 3/ 4, where 3 is the numerator and 4 is the denominator.	Image Source
		2

Improper Fractions
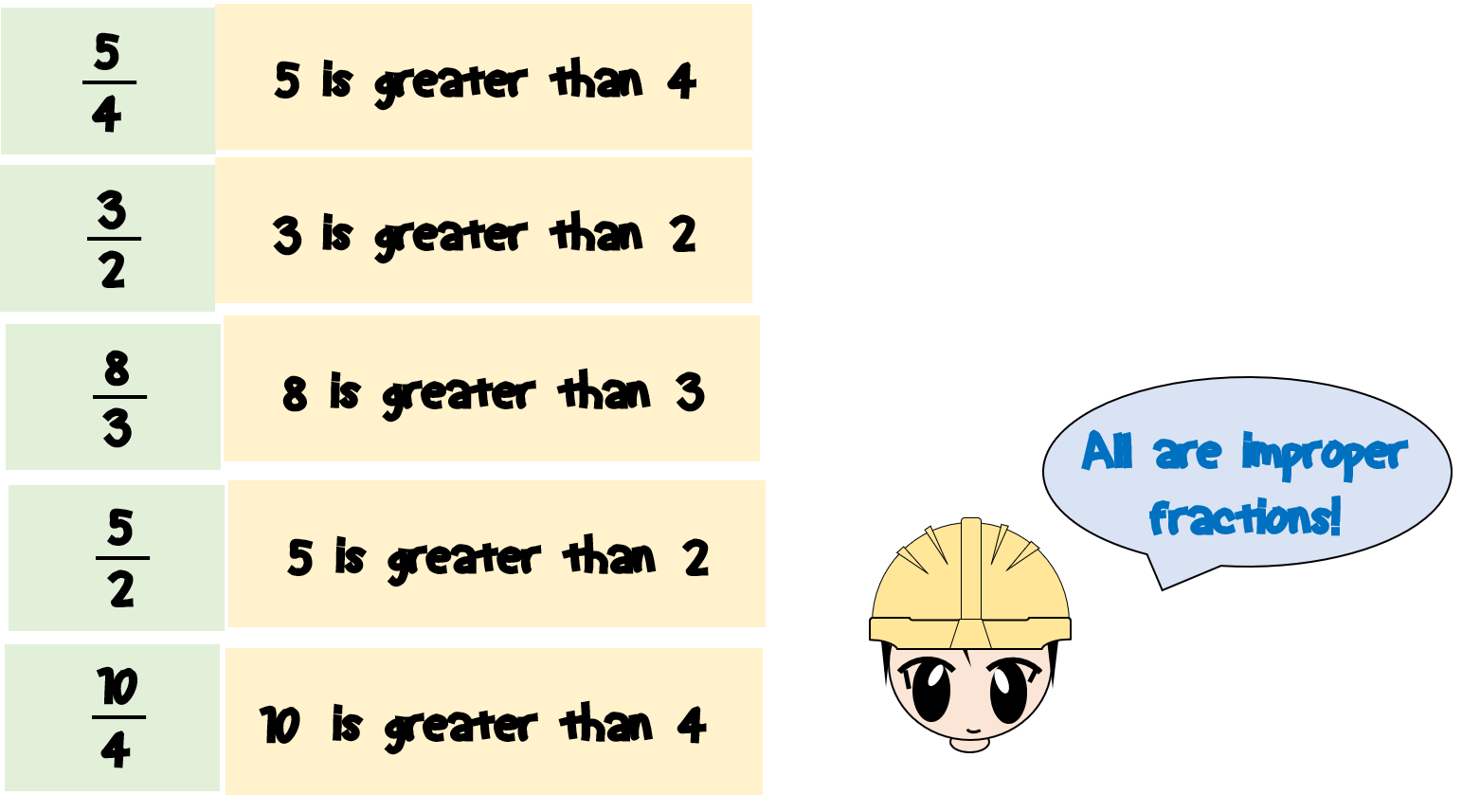
Improper fractions have a numerator that is equal to or greater than the denominator. The value of an improper fraction can be equal to or greater than 1. Example: 5/ 3, where 5 is the numerator and 3 is the denominator.	Image Source
		3

Mixed Numbers
Mixed numbers are a combination of a whole number and a proper fraction. They can be converted into improper fractions and vice versa. Example: 2 1/ 2, where 2 is the whole number, 1 is the numerator, and 2 is the denominator.	Image Source
		4

Equivalent Fractions
Equivalent fractions have different numerators and denominators but represent the same value. They can be found by multiplying or dividing both the numerator and denominator by the same number. Example: 1/ 2 and 2/ 4 are equivalent fractions.	Image Source
		5

Like Fractions
Like fractions have the same denominators. They can be added or subtracted by simply adding or subtracting their numerators. Example: 3/ 5 + 2/ 5 = 5/ 5 = 1.
		6

Unlike Fractions
Unlike fractions have different denominators. They need to be converted into like fractions before adding or subtracting them. Example: 1/ 3 + 1/ 4 = 4/ 12 + 3/ 12 = 7/ 12.
		7

Proper Improper Fractions
Proper improper fractions are fractions where the numerator is greater than or equal to the denominator. They can be converted into mixed numbers. Example: 7/ 4 can be converted into 1 3/ 4.	Image Source
		8

Reciprocal Fractions
Reciprocal fractions are fractions in which the numerator and denominator are switched. When multiplied together, they always result in 1. Example: The reciprocal of 3/ 4 is 4/ 3.	Image Source
		9

Conclusion
Fractions are an essential part of mathematics and everyday life. Understanding the different types of fractions helps in solving problems and making calculations. Practice and repetition are key to mastering fractions.	Image Source
		10

Join the SlideMake Community