Triple Integrals Presentation
| Introduction | ||
|---|---|---|
| Triple integrals are an extension of double integrals in three dimensions. They are used to calculate the volume, mass, or average value of a function over a three-dimensional region. Triple integrals are denoted by ∭f(x, y, z) dV, where f(x, y, z) is the integrand and dV represents the infinitesimal volume element. | ||
| 1 | ||
| Triple Integral Bounds | ||
|---|---|---|
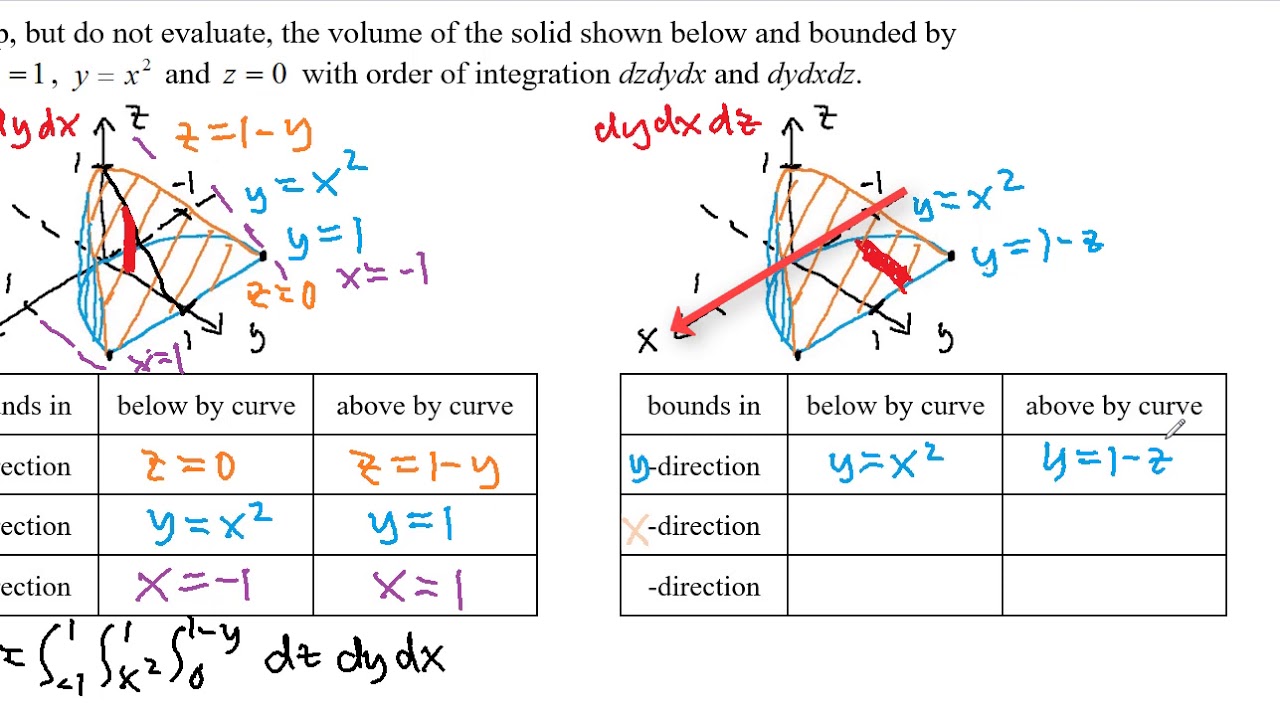
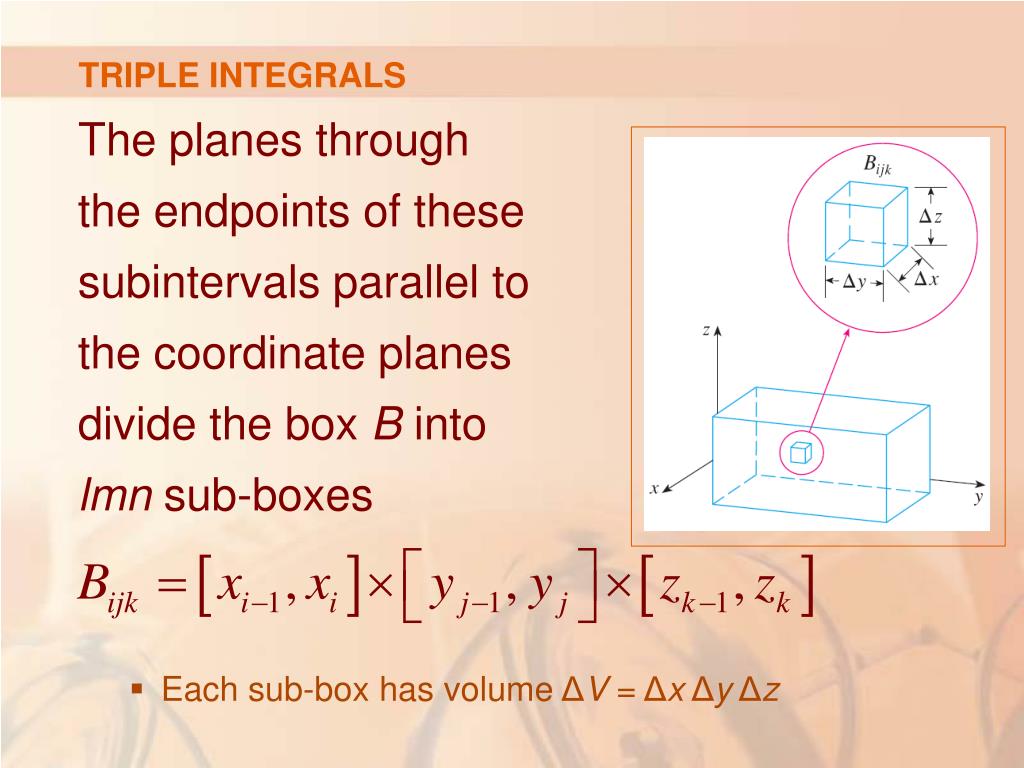
| The bounds of a triple integral define the region of integration in three-dimensional space. The region can be defined using Cartesian, cylindrical, or spherical coordinates. Cartesian coordinates: x_min ≤ x ≤ x_max, y_min ≤ y ≤ y_max, z_min ≤ z ≤ z_max. | ||
| 2 | ||
| Evaluation of Triple Integrals | ||
|---|---|---|
| Triple integrals can be evaluated using iterated integrals by integrating one variable at a time. The order of integration can be varied depending on the symmetry of the region or the simplicity of the integrand. When the region is simple, using the order of integration that matches the natural order of the coordinates can simplify the calculations. | ||
| 3 | ||
| Applications of Triple Integrals | ||
|---|---|---|
| Volume calculation: Triple integrals can be used to calculate the volume of irregular shapes or solid objects. Mass calculation: By incorporating a density function into the integrand, triple integrals can be used to calculate the mass of an object. Average value calculation: Triple integrals can also be used to calculate the average value of a function over a three-dimensional region. | ||
| 4 | ||
| Properties of Triple Integrals | ||
|---|---|---|
| Linearity: Triple integrals satisfy the linearity property, allowing for easy calculations when the integrand can be expressed as a sum of multiple functions. Change of variables: Triple integrals can be transformed using a change of variables, which can simplify the calculations or help to change the coordinate system. Symmetry: Sometimes, the symmetry of the region or the integrand can be exploited to simplify the triple integral. | ||
| 5 | ||
| Conclusion | ||
|---|---|---|
| Triple integrals are powerful tools in mathematics and physics for calculating volumes, masses, and average values over three-dimensional regions. Understanding the bounds, evaluation methods, and properties of triple integrals is essential for their successful application. With practice and familiarity, triple integrals can become a valuable tool in solving a wide range of mathematical and physical problems. | ||
| 6 | ||