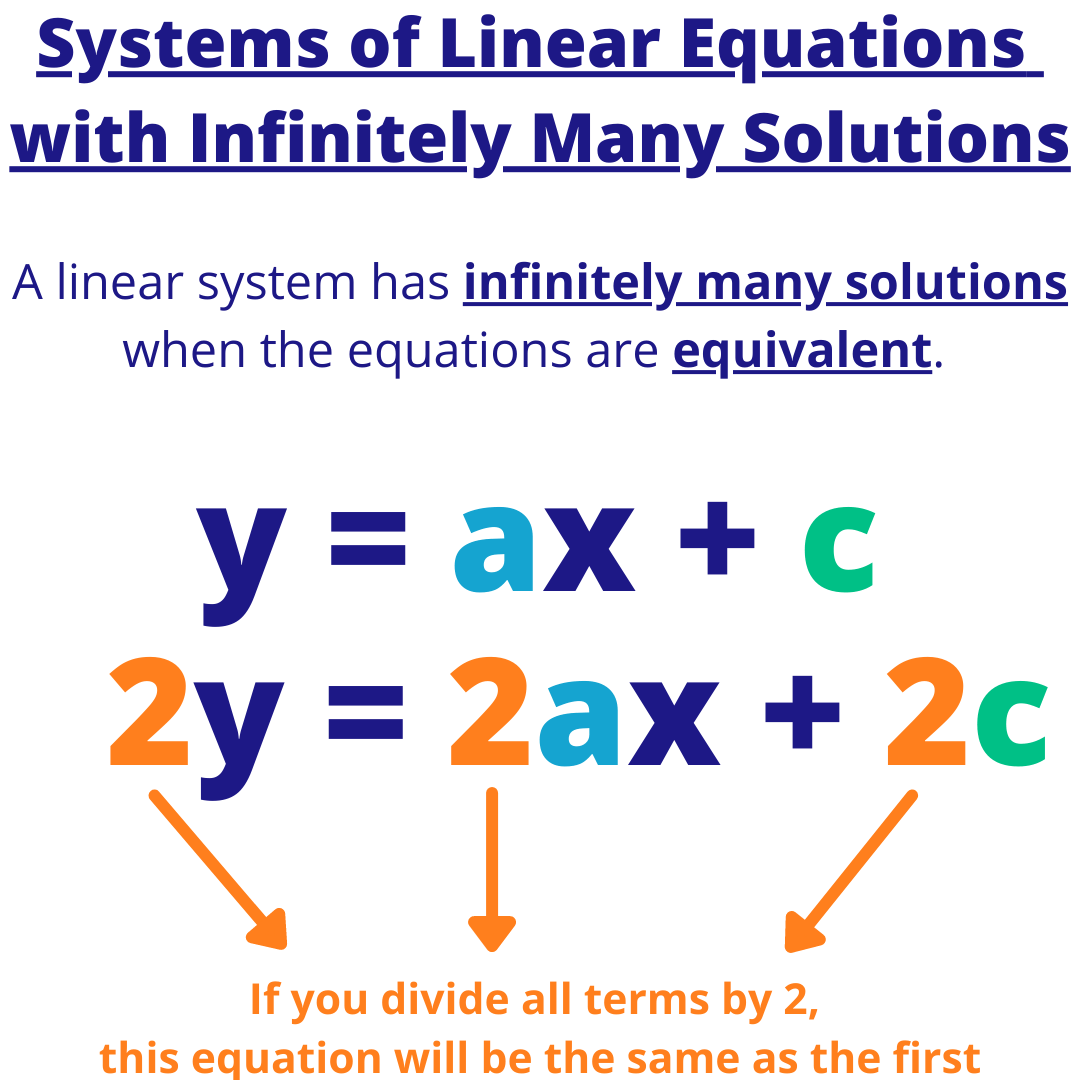System Of Linear Equations And Non Homogenous Equations Presentation

Introduction to System of Linear Equations and Non-Homogeneous Equations
System of linear equations involves a set of equations with linear terms. Non-homogeneous equations have non-zero constants on the right-hand side. Solving these equations helps find the values of variables that satisfy all the equations simultaneously.	Image Source
		1

Solving System of Linear Equations
Gaussian elimination is a common method to solve systems of linear equations. It involves transforming the system into an equivalent triangular form. Back substitution is then used to find the values of variables starting from the last equation.	Image Source
		2

Properties of System of Linear Equations
A system of linear equations can have unique, infinitely many, or no solutions. Unique solution occurs when the system has the same number of equations as variables. Infinitely many solutions occur when the equations are dependent or consistent.	Image Source
		3

Matrix Representation of System of Linear Equations
A system of linear equations can be represented using matrices. Coefficients of variables form the coefficient matrix. Constants on the right-hand side form the constant matrix.	Image Source
		4

Non-Homogeneous Equations
Non-homogeneous equations have non-zero constants on the right-hand side. These equations can be solved using the same methods as system of linear equations. The solution consists of the particular solution and the homogeneous solution.	Image Source
		5

Particular Solution
Particular solution is a specific solution that satisfies the non-homogeneous equation. It can be found using methods like undetermined coefficients or variation of parameters. The particular solution represents a specific set of values for the variables.	Image Source
		6

Homogeneous Solution
Homogeneous solution satisfies the associated homogeneous equation. It represents a set of solutions that make the non-homogeneous equation equal to zero. The homogeneous solution is obtained by setting the constants in the particular solution to zero.	Image Source
		7

Summary and Applications
Solving system of linear equations and non-homogeneous equations is crucial in various fields like engineering, economics, and physics. The properties of these equations help analyze and model real-world problems. Understanding these concepts and techniques allows for efficient problem-solving and decision-making.	Image Source
		8