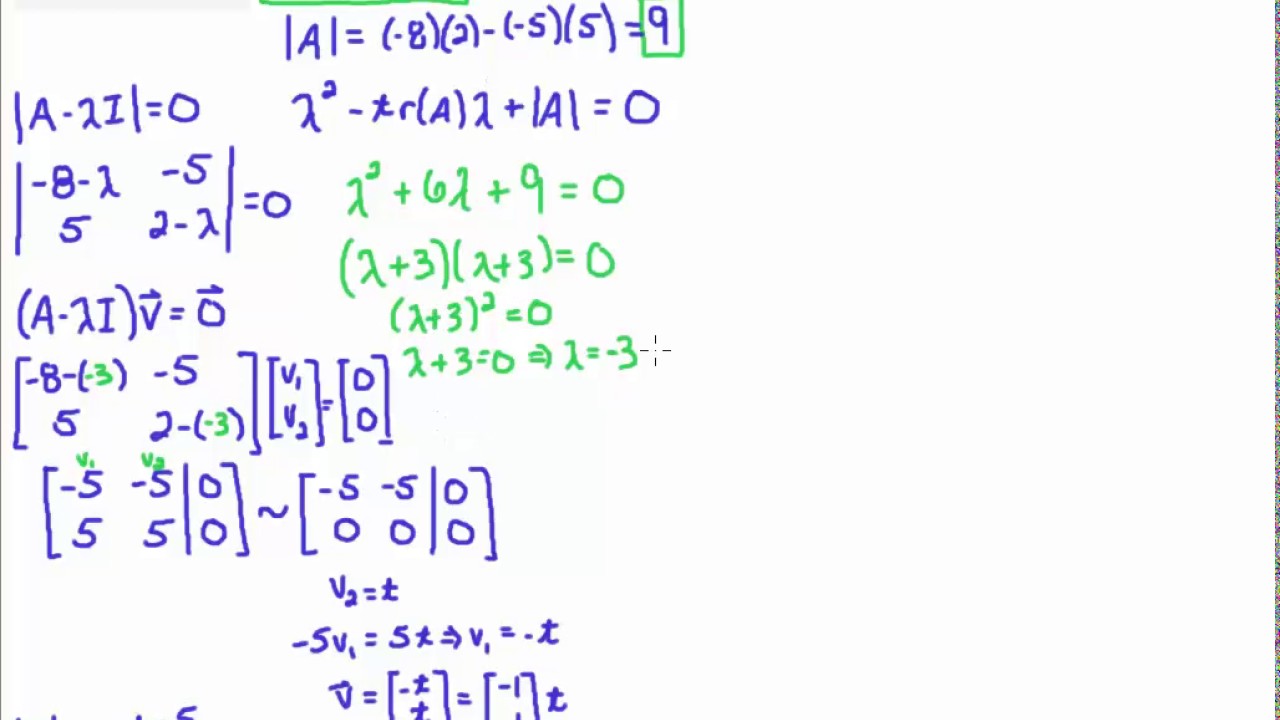Role Of Vibration Analysis Eigen Values & Eigen Vectors Presentation

Introduction to Vibration Analysis Eigenvalues & Eigenvectors
Vibration analysis is a powerful tool used to study the behavior of mechanical systems. Eigenvalues and eigenvectors play a crucial role in understanding and analyzing vibrations. In this presentation, we will explore the significance of eigenvalues and eigenvectors in vibration analysis.	Image Source
		1

Understanding Eigenvalues
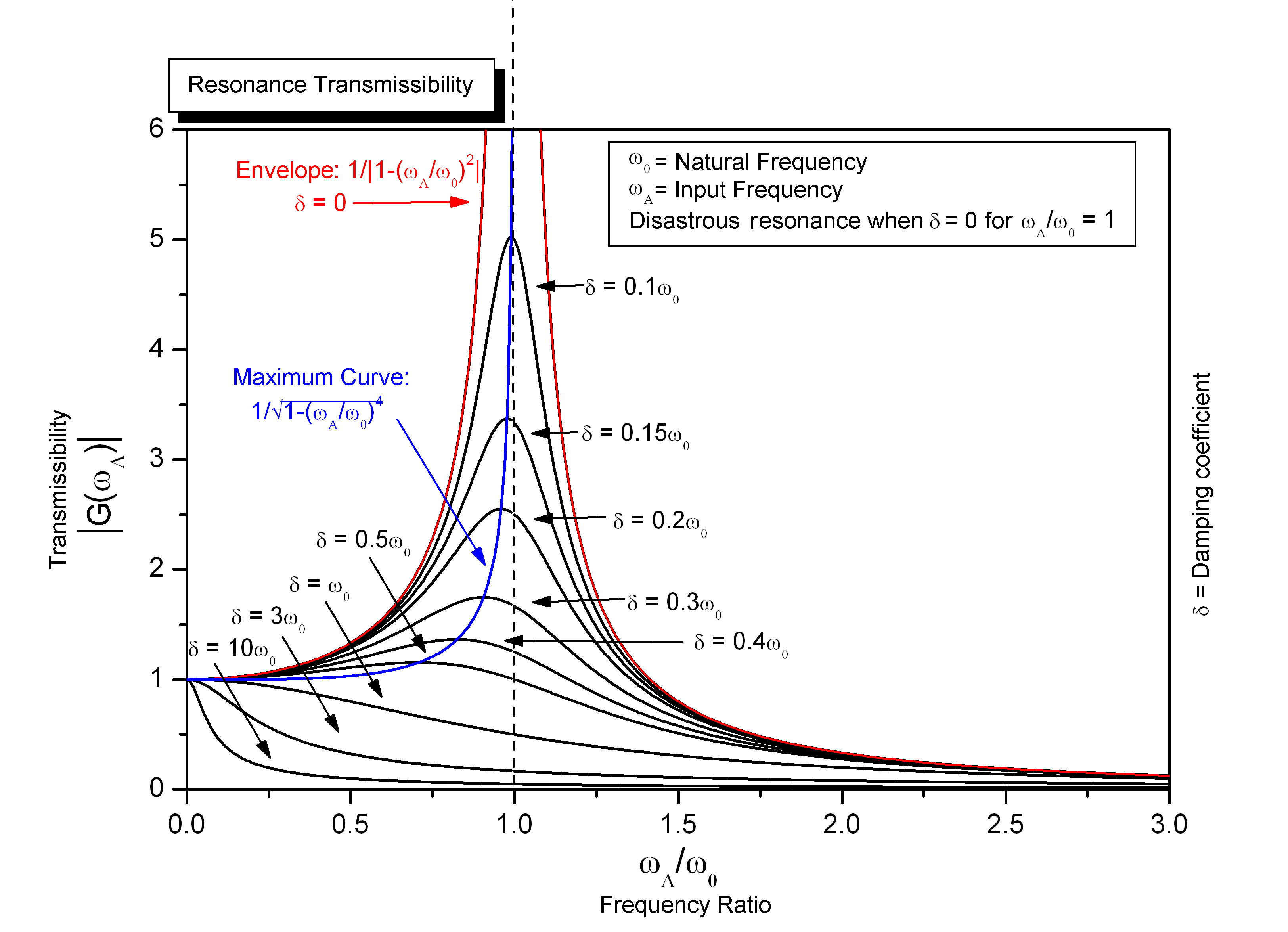
Eigenvalues represent the natural frequencies of a vibrating system. They are the values for which a linear transformation does not change the direction of a vector. Eigenvalues are obtained by solving the characteristic equation of the system.	Image Source
		2

Significance of Eigenvalues in Vibration Analysis
Eigenvalues help identify the resonant frequencies of a vibrating system. Resonant frequencies are critical because they can lead to excessive vibrations and potential failure. By analyzing the eigenvalues, engineers can determine the system's response to external forces at specific frequencies.	Image Source
		3

Understanding Eigenvectors
Eigenvectors represent the mode shapes of a vibrating system. They are the vectors that do not change their direction during a linear transformation. Eigenvectors are obtained by solving the eigenvalue problem of the system.	Image Source
		4

Significance of Eigenvectors in Vibration Analysis
Eigenvectors help visualize the deformation patterns of a vibrating system. They provide insights into how different parts of the system move and vibrate relative to each other. Analyzing eigenvectors enables engineers to identify potential areas of stress concentration and design improvements.	Image Source
		5

Relationship between Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are interconnected in vibration analysis. Each eigenvalue corresponds to a unique eigenvector and vice versa. Together, they define the behavior of the system and its response to vibrations.	Image Source
		6

Eigenvalue-Eigenvector Pairing
The pairing of eigenvalues and eigenvectors is essential for vibration analysis. Each eigenvalue-eigenvector pair represents a distinct mode of vibration. Engineers can evaluate the significance of each mode and its impact on the system's overall response.	Image Source
		7

Using Eigenvalues and Eigenvectors for System Monitoring
Eigenvalue analysis allows for early detection of potential faults or structural damage. By monitoring changes in eigenvalues, engineers can identify shifts in the system's natural frequencies. Eigenvector analysis helps pinpoint the regions of the system experiencing the most significant changes.	Image Source
		8

Application of Eigenvalues and Eigenvectors in Structural Health Monitoring
Eigenvalues and eigenvectors are crucial in structural health monitoring. Changes in eigenvalues can indicate the presence of cracks, fatigue, or other structural issues. Eigenvectors provide valuable information about the location and severity of the damage.	Image Source
		9

Conclusion
Eigenvalues and eigenvectors are fundamental to vibration analysis. They provide insights into the behavior, response, and health of mechanical systems. By understanding and analyzing these values, engineers can optimize the design and performance of vibrating systems.	Image Source
		10

References (download PPTX file for details)
Smith, J. (2019). Vibration Analysis: Underst... Rao, S. S. (2011). Mechanical Vibrations (5th... Your third bullet...
		11

Join the SlideMake Community