Role Of Computer Graphic By Matrices- Homogeneous Presentation

Introduction to Computer Graphics and Matrices
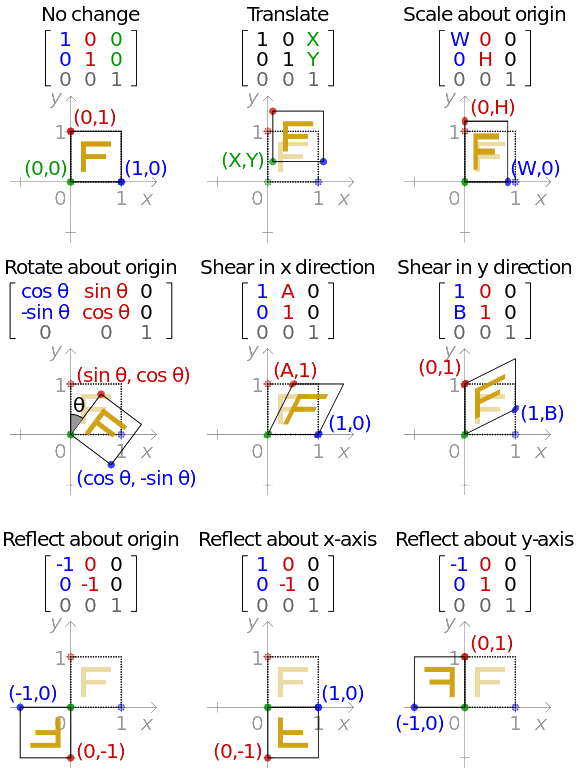
Computer graphics is the field of visualizing and manipulating digital images using algorithms and mathematical models. Matrices, specifically homogeneous matrices, play a crucial role in computer graphics for transformations and rendering. Homogeneous matrices are 4x4 matrices that allow us to represent translation, rotation, scaling, and shearing operations.	Image Source
		1

Coordinate Systems and Transformations
Coordinate systems define a reference frame to position and orient objects in the 3D world. Homogeneous matrices can transform coordinates from one coordinate system to another. Transformations include translation, rotation, scaling, and shearing, affecting an object's position, orientation, and size.	Image Source
		2

Transformation Matrices
Homogeneous transformation matrices combine translation, rotation, and scaling into a single matrix. Translation matrices shift objects in the x, y, and z-axis. Rotation matrices rotate objects around a specific axis, such as x, y, or z.	Image Source
		3

Composite Transformations
Composite transformations combine multiple transformations into a single matrix. The order of transformations affects the final result, as transformations are not commutative. By multiplying multiple transformation matrices, we can achieve complex transformations.
		4

Projection Matrices
Projection matrices map 3D objects onto a 2D plane, simulating perspective. Common types of projection matrices include orthographic and perspective projections. Perspective projection matrices consider the distance between the viewer and the object, creating a more realistic representation.	Image Source
		5

Homogeneous Coordinates
Homogeneous coordinates extend the 3D space to 4D, allowing for efficient matrix operations. Homogeneous coordinates use a fourth coordinate, w, to represent translations and perspective projection. Converting between homogeneous and Cartesian coordinates involves dividing by w.	Image Source
		6

Transformation Pipelines
Transformation pipelines describe the sequence of transformations applied to an object. These pipelines typically involve model, view, and projection matrices. The final result is the transformation of an object from its model space to the screen space.	Image Source
		7

Lighting and Shading
Homogeneous matrices also play a role in lighting and shading calculations. Normal transformation matrices allow us to transform surface normals to the correct orientation. Lighting calculations involve transforming light sources and surface normals into homogeneous space.	Image Source
		8

Matrix Manipulation Libraries
Various programming libraries provide matrix manipulation functionalities for computer graphics. Popular matrix libraries include OpenGL, DirectX, and WebGL. These libraries handle matrix operations efficiently, allowing for real-time rendering and visualizations.	Image Source
		9

Conclusion
Homogeneous matrices are essential for computer graphics, enabling transformations, projections, and lighting calculations. They provide a powerful mathematical framework for representing and manipulating 3D objects. Understanding the role of matrices in computer graphics is fundamental for creating realistic and immersive visual experiences.	Image Source
		10

Join the SlideMake Community