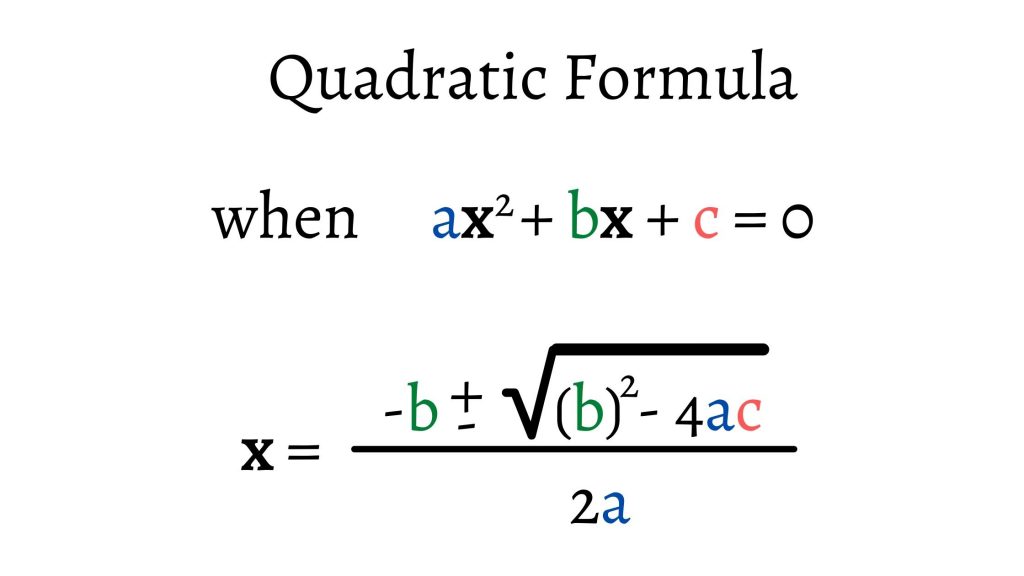Quadratic Equation Presentation
| Introduction to Quadratic Equations | ||
|---|---|---|
| Quadratic equations are algebraic equations that contain a variable raised to the power of 2. The general form of a quadratic equation is ax^2 + bx + c = 0, where a, b, and c are constants. Quadratic equations can have one, two, or no real solutions. | ||
| 1 | ||
| The Quadratic Formula | ||
|---|---|---|
| The quadratic formula is a method used to find the solutions to any quadratic equation. It is given by x = (-b ± √(b^2 - 4ac)) / (2a). The discriminant, b^2 - 4ac, determines the nature of the solutions. | ||
| 2 | ||
| Nature of Solutions | ||
|---|---|---|
| If the discriminant is positive, the quadratic equation has two distinct real solutions. If the discriminant is zero, the quadratic equation has one real solution (also called a repeated root). If the discriminant is negative, the quadratic equation has no real solutions, only complex solutions. | ||
| 3 | ||
| Graphical Representation | ||
|---|---|---|
| Quadratic equations can be graphically represented by a parabola. The shape of the parabola depends on the value of the coefficient a. If a > 0, the parabola opens upwards. If a < 0, the parabola opens downwards. | ||
| 4 | ||
| Vertex of a Quadratic Equation | ||
|---|---|---|
| The vertex of a quadratic equation is the point where the parabola reaches its maximum or minimum value. The x-coordinate of the vertex can be found using the formula x = -b / (2a). The y-coordinate of the vertex can be found by substituting the x-coordinate into the quadratic equation. | ||
| 5 | ||
| Factoring Quadratic Equations | ||
|---|---|---|
| Factoring is a method used to solve quadratic equations by finding two binomials that multiply to give the quadratic expression. Quadratic equations can be factored by using the zero-product property. Factoring is an efficient method when the quadratic equation can be easily factored. | ||
| 6 | ||
| Completing the Square | ||
|---|---|---|
| Completing the square is a method used to solve quadratic equations by manipulating the equation into a perfect square trinomial. The process involves adding or subtracting a constant term to both sides of the equation. Completing the square is useful when factoring is not possible or desired. | ||
| 7 | ||
| Applications of Quadratic Equations | ||
|---|---|---|
| Quadratic equations are widely used in physics to model projectile motion, such as the trajectory of a thrown object. They are also used in engineering to model parabolic shapes, such as the design of bridges and arches. Quadratic equations find applications in economics, biology, computer science, and many other fields. | ||
| 8 | ||
| Quadratic Equations in Real Life | ||
|---|---|---|
| Quadratic equations can be used to solve real-life problems, such as calculating the maximum profit or minimum cost. They can be used to determine the height, range, or time of flight of a projectile. Quadratic equations can help in optimizing various processes, such as finding the maximum area of a rectangular garden given a fixed perimeter. | ||
| 9 | ||
| Summary and Conclusion | ||
|---|---|---|
| Quadratic equations are a fundamental concept in algebra and have numerous applications in various fields. They can be solved using the quadratic formula, factoring, or completing the square. Understanding quadratic equations is essential for solving real-life problems and modeling various phenomena. | ||
| 10 | ||