Physical Significance Of Curl Presentation

Introduction to Curl
The curl is a mathematical operator used to describe the rotation or circulation of a vector field. It measures the tendency of a vector field to circulate around a point. The curl is a vector quantity that is defined as the cross product of the gradient of a vector field.	Image Source
		1

Mathematical Definition of Curl
The curl of a vector field F is given by the cross product of the del operator (∇) and the vector field F. Mathematically, curl(F) = ∇ x F. The curl is a vector that represents the rotation of the field in three-dimensional space.	Image Source
		2

Physical Interpretation of Curl
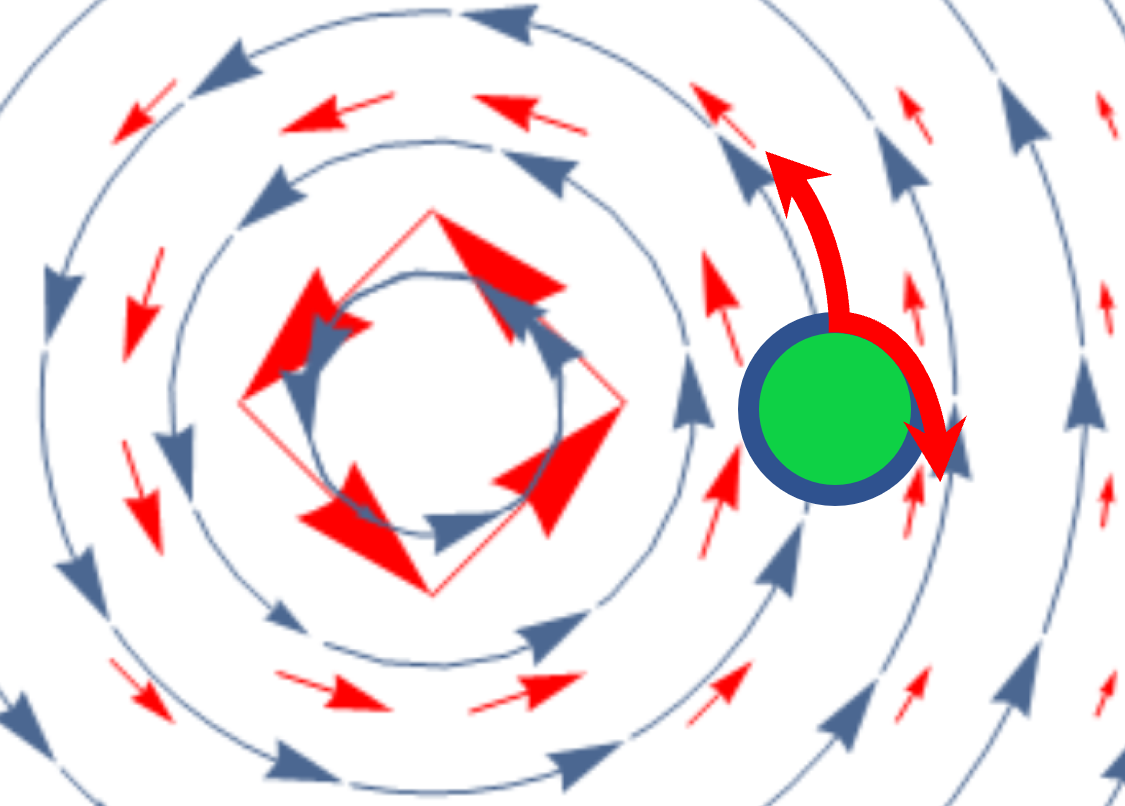
The curl describes the circulation or rotational behavior of a vector field. It indicates the presence and strength of vortices or rotational motion within a region. The magnitude of the curl represents the rate of rotation or circulation at a given point.	Image Source
		3

Applications in Fluid Dynamics
In fluid dynamics, the curl is used to describe the vorticity of a fluid flow. Vorticity is a measure of the local spinning or rotation of fluid particles. The curl of the velocity field provides information about the vorticity distribution within the fluid.	Image Source
		4

Magnetic Field and Curl
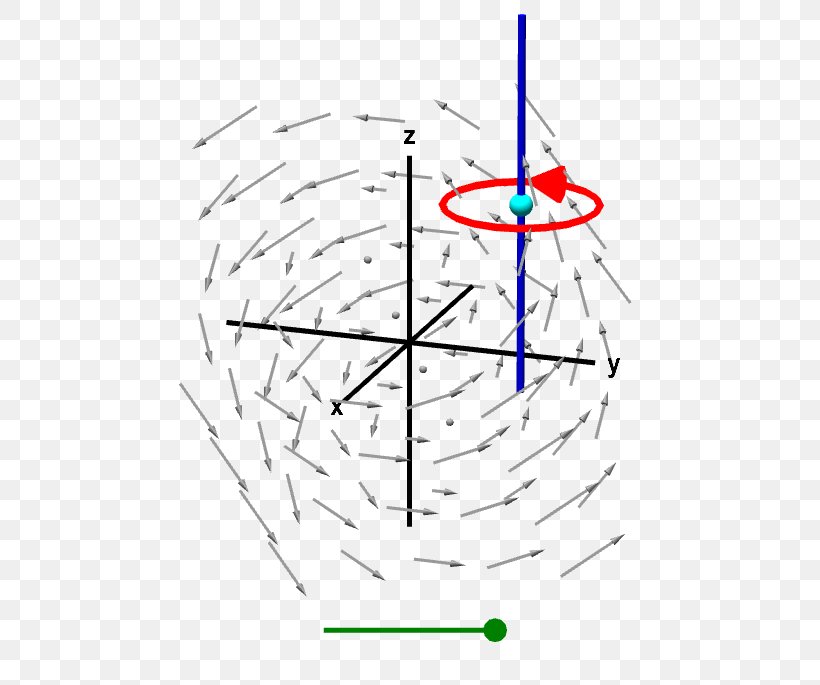
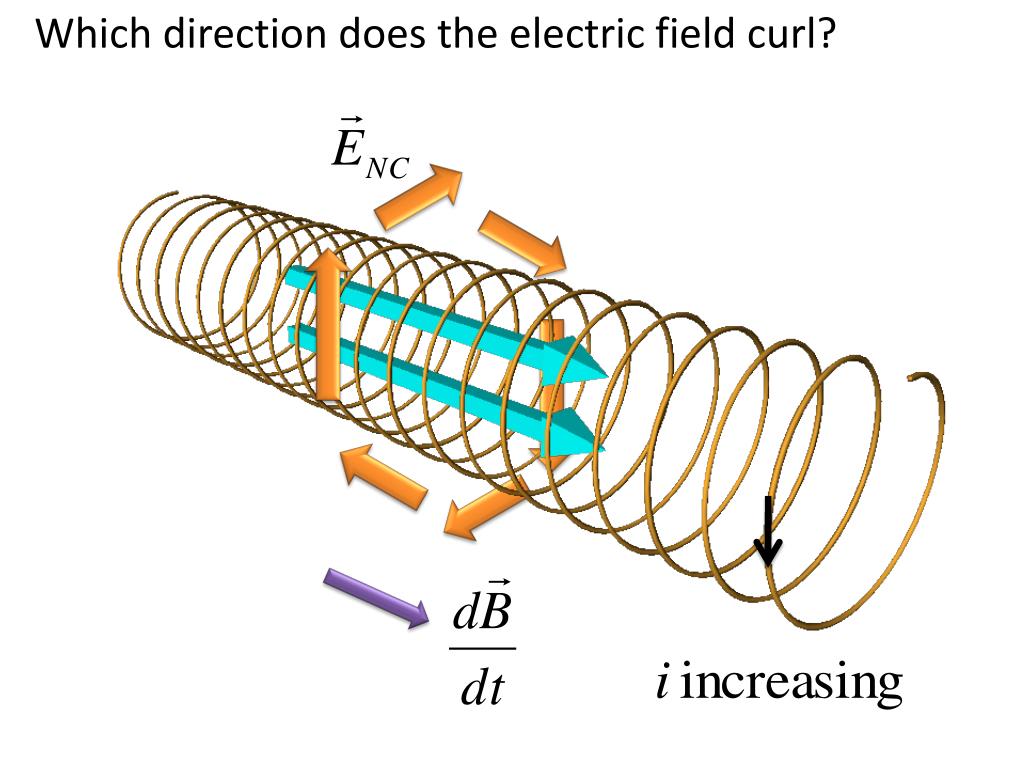
In electromagnetism, the curl of the magnetic field represents the presence of magnetic vortices or circulating currents. The curl of the magnetic field is related to the current density in Ampere's law. The magnetic field lines form closed loops, indicating the presence of a non-zero curl.	Image Source
		5

Conservation Laws and Curl
The curl plays a role in the conservation laws of physics. In the context of fluid dynamics, the curl of the velocity field is related to the conservation of angular momentum. The curl also appears in the equations of electromagnetism, such as Faraday's law and Ampere's law.	Image Source
		6

Vector Analysis and Curl
The curl is an important concept in vector analysis and is used to study vector fields in mathematics and physics. It helps in understanding the behavior of vector fields, particularly their rotational or circulating patterns. The curl can be used to solve problems involving circulation, rotation, and vortices in various fields of science and engineering.	Image Source
		7

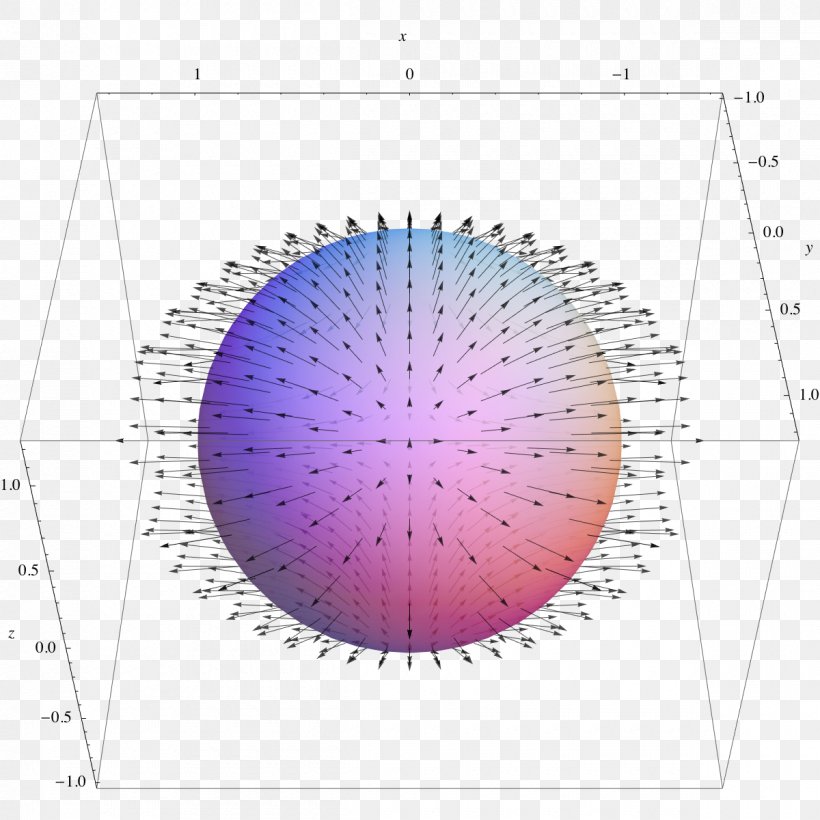
Visualization of Curl
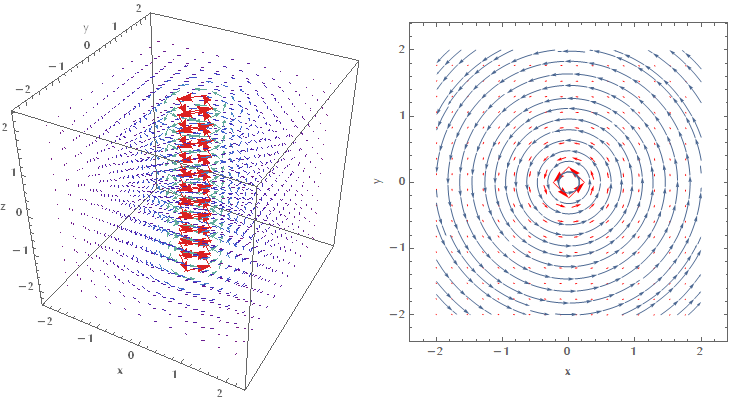
The curl can be visually represented using vector plots or streamlines. The magnitude of the curl is represented by the length of the vectors or the density of streamlines. Visualization techniques help in understanding the rotational behavior of vector fields.	Image Source
		8

Relationship with Divergence
The curl and divergence are related concepts in vector calculus. While the curl represents the rotation or circulation of a vector field, the divergence measures the expansion or contraction of the field. The curl and divergence can be used together to fully characterize a vector field.	Image Source
		9

Summary
The curl is a mathematical operator that describes the rotational or circulating behavior of a vector field. It has physical significance in fluid dynamics, electromagnetism, and conservation laws. Visualization techniques and vector analysis help in understanding and analyzing the curl of a vector field.	Image Source
		10

References (download PPTX file for details)
Stewart, J. (2015). Calculus: Early Transcend... Arfken, G. B., Weber, H. J., & Harris, F. E. ... Spiegel, M. R., & Lipschutz, S. (2009). Vecto...
		11

Join the SlideMake Community