Numbering System With Binary And Octel Presentation

Introduction to Numbering Systems with Binary and Octal
The binary numbering system is a base-2 system that uses only two digits, 0 and 1. Octal numbering system is a base-8 system that uses digits from 0 to 7. Both systems are widely used in computer science and digital electronics.	Image Source
		1

Understanding Binary Numbering System
In the binary system, each digit represents a power of 2. Binary numbers are composed of bits (binary digits). Binary numbers are essential in representing and manipulating digital data.	Image Source
		2

Converting Decimal to Binary
To convert a decimal number to binary, divide the number by 2 and keep track of the remainders. Repeat the process until the quotient becomes 0. The binary representation is the sequence of remainders read from bottom to top.	Image Source
		3

Converting Binary to Decimal
To convert a binary number to decimal, assign each digit a power of 2. Multiply each digit by its corresponding power of 2. Sum up the results to obtain the decimal equivalent.	Image Source
		4

Understanding Octal Numbering System
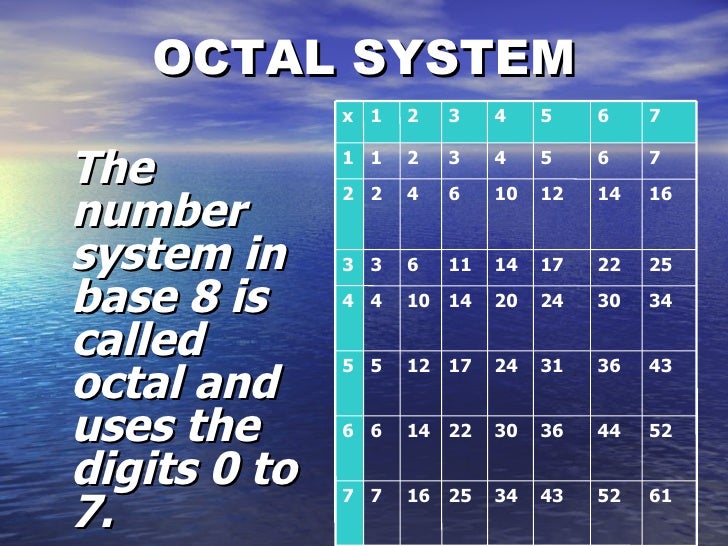
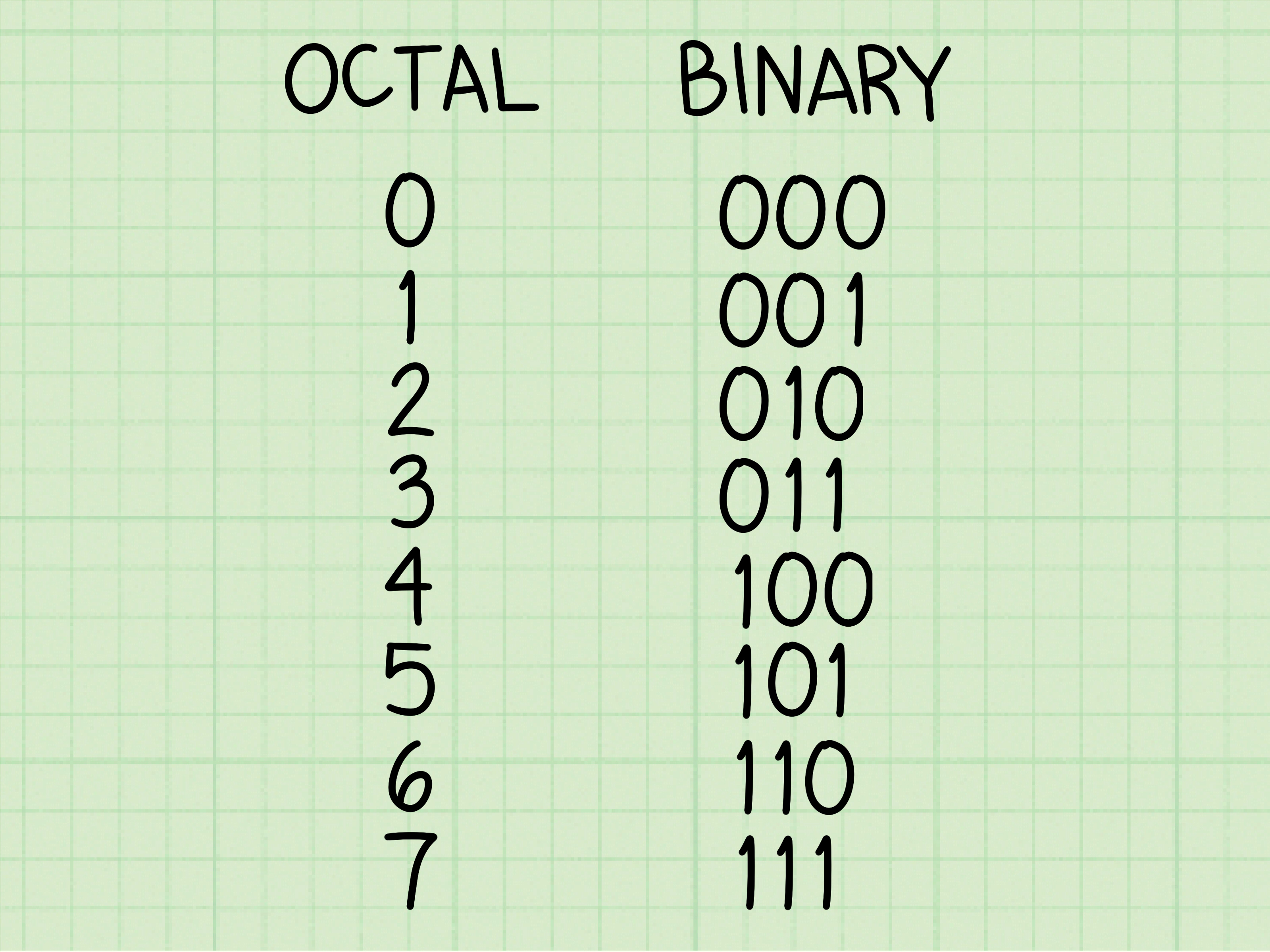
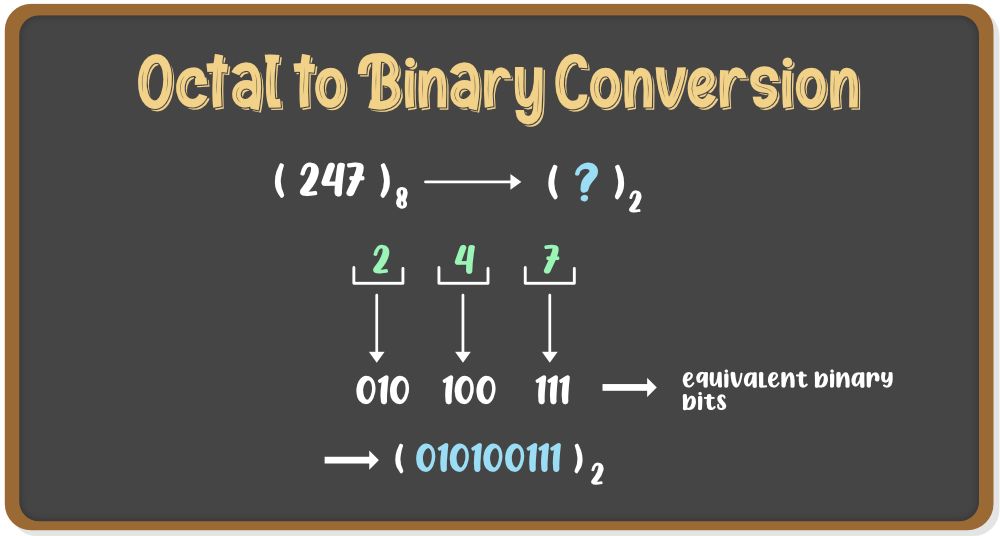
Octal numbers are base-8 numbers that use digits from 0 to 7. Each digit in an octal number represents a power of 8. Octal numbers are shorter than binary numbers, making them useful in certain applications.	Image Source
		5

Converting Decimal to Octal
To convert a decimal number to octal, divide the number by 8 and keep track of the remainders. Repeat the process until the quotient becomes 0. The octal representation is the sequence of remainders read from bottom to top.	Image Source
		6

Converting Octal to Decimal
To convert an octal number to decimal, assign each digit a power of 8. Multiply each digit by its corresponding power of 8. Sum up the results to obtain the decimal equivalent.	Image Source
		7

Binary and Octal in Computer Science
Binary numbers are fundamental in computer science as they represent the on/ off states of electronic circuits. Octal numbers are used in computer systems where groupings of binary digits are required. Converting between binary and octal can simplify certain computational tasks.	Image Source
		8

Advantages and Disadvantages of Binary and Octal
Binary numbers provide precise representation of data but can be cumbersome. Octal numbers offer a more compact representation but lack precision. The choice between binary and octal depends on the specific requirements of a given application.	Image Source
		9

Summary and Key Takeaways
Binary and octal numbering systems are widely used in computer science and digital electronics. Binary numbers are base-2 and use only 0 and 1, while octal numbers are base-8 and use digits from 0 to 7. Converting between decimal, binary, and octal numbers is essential in various computational tasks.	Image Source
		10

References (download PPTX file for details)
Smith, J. (2018). Binary and Octal Number Sys... Johnson, A. (2019). Introduction to Computer ... Digital Electronics. (2020). Binary and Octal...
		11