Merge Sort Presentation
| Introduction to Merge Sort | ||
|---|---|---|
| Merge sort is a popular sorting algorithm. It follows the divide-and-conquer approach. It has a time complexity of O(n log n). | ||
| 1 | ||
| How Merge Sort Works | ||
|---|---|---|
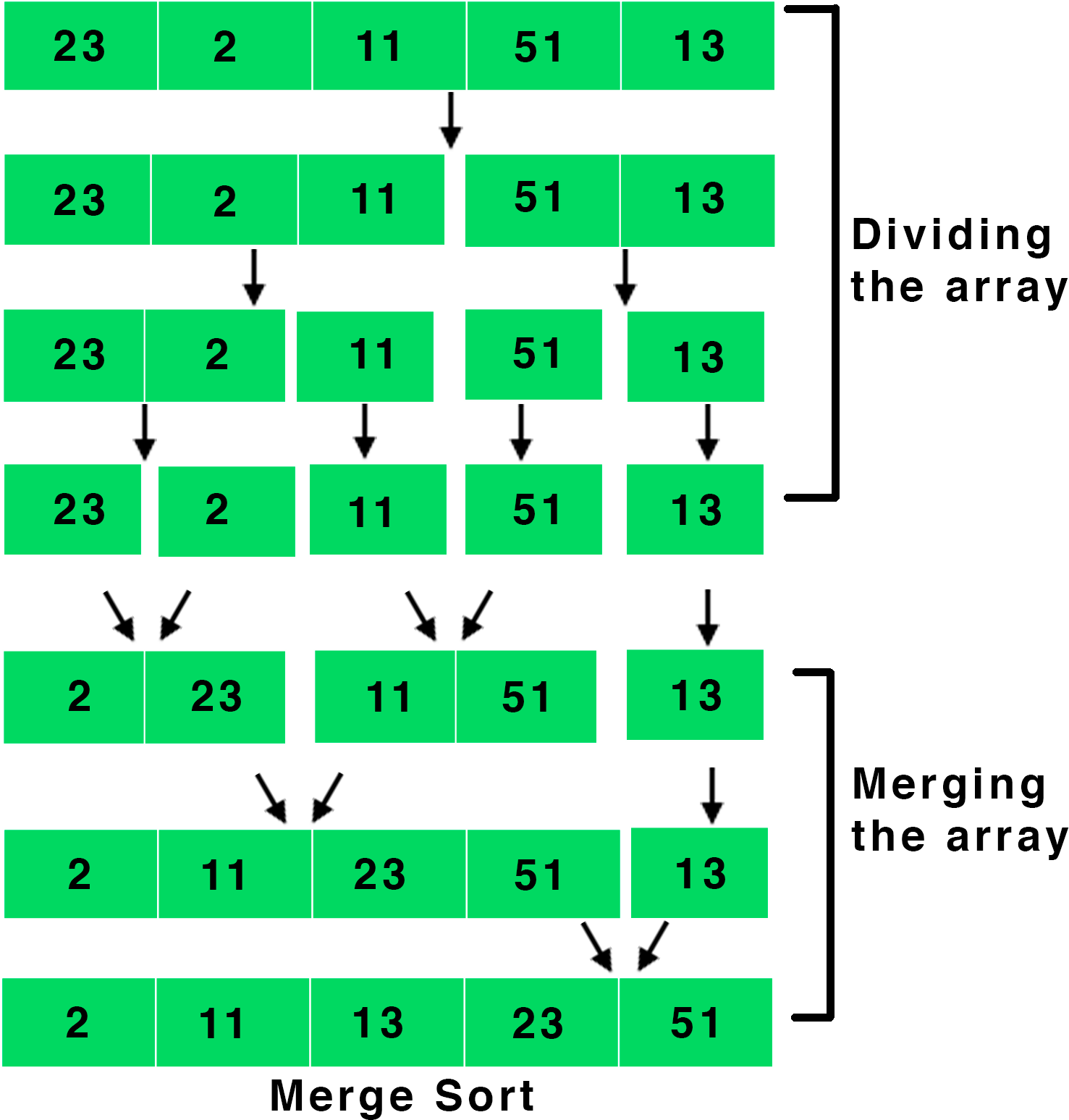
| Merge sort divides the unsorted list into smaller sublists recursively. It then merges these sublists into a sorted list. The merging process combines two sorted sublists into one. | ||
| 2 | ||
| Divide Step of Merge Sort | ||
|---|---|---|
| The divide step involves splitting the original list into two halves. This process continues until each sublist contains only one element. The divide step is done recursively. | ||
| 3 | ||
| Merge Step of Merge Sort | ||
|---|---|---|
| The merge step involves merging the sorted sublists into a single sorted list. It compares the elements from the two sublists and places them in the correct order. This process continues until all elements are merged. | ||
| 4 | ||
| Visualization of Merge Sort | ||
|---|---|---|
| Imagine sorting a deck of cards by dividing it into smaller piles and merging them back together. The merge step involves comparing and placing the cards in the correct order. This process continues until the entire deck is sorted. | ||
| 5 | ||
| Advantages of Merge Sort | ||
|---|---|---|
| Merge sort is a stable sorting algorithm, meaning it preserves the relative order of equal elements. It is efficient for handling large data sets. Merge sort guarantees a worst-case time complexity of O(n log n). | ||
| 6 | ||
| Disadvantages of Merge Sort | ||
|---|---|---|
| Merge sort requires additional space to store the temporary sublists during the merging process. It may not be the best choice for small data sets or when memory usage is a concern. The recursive nature of merge sort can lead to stack overflow errors for very large lists. | ||
| 7 | ||
| Applications of Merge Sort | ||
|---|---|---|
| Merge sort is commonly used in external sorting, where data is too large to fit into memory. It is widely used in programming languages and libraries for sorting arrays and lists. Merge sort is also used in merge join algorithms in database systems. | ||
| 8 | ||
| Comparison with Other Sorting Algorithms | ||
|---|---|---|
| Merge sort has a consistent time complexity of O(n log n) for all cases. It is more efficient than bubble sort and insertion sort for large data sets. Quick sort has a better average-case performance but can have a worst-case time complexity of O(n^2). | ||
| 9 | ||
| Conclusion | ||
|---|---|---|
| Merge sort is a reliable and efficient sorting algorithm. It follows a divide-and-conquer approach and guarantees a worst-case time complexity of O(n log n). Understanding merge sort is essential for every programmer's toolkit. | ||
| 10 | ||