Mathematics In Artificial Intelligence Presentation

Introduction to Mathematics in Artificial Intelligence
Mathematics plays a crucial role in the development and implementation of Artificial Intelligence (AI) systems. AI relies on mathematical concepts and algorithms to process and analyze large amounts of data. Mathematical models provide a foundation for building intelligent systems and making informed decisions.	Image Source
		1

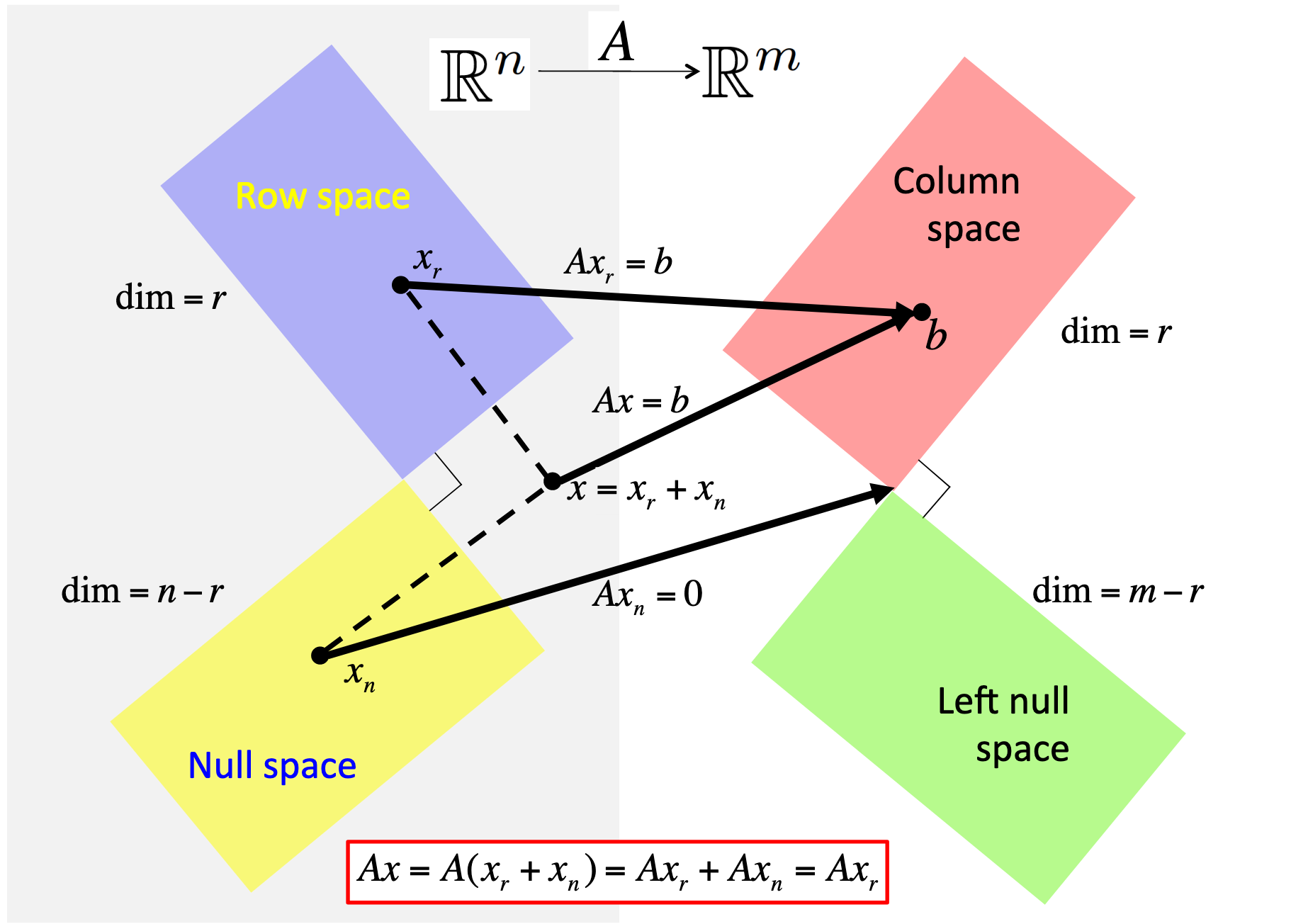
Linear Algebra in AI
Linear algebra is fundamental to AI as it deals with vectors, matrices, and linear transformations. In AI, linear algebra is used for tasks such as dimensionality reduction, image recognition, and natural language processing. Concepts like eigenvectors and eigenvalues are employed to understand patterns and extract meaningful information.	Image Source
		2

Calculus in AI
Calculus is essential for optimization problems in AI, such as finding the minimum or maximum of a function. Techniques like gradient descent use calculus to train machine learning models. Calculus also helps in understanding the rate of change and modeling dynamic systems in AI.	Image Source
		3

Probability and Statistics in AI
Probability theory is crucial for dealing with uncertainty in AI systems. Statistical techniques, such as hypothesis testing and regression analysis, are used to analyze and interpret data. Bayesian networks utilize probability theory to model and reason under uncertainty.	Image Source
		4

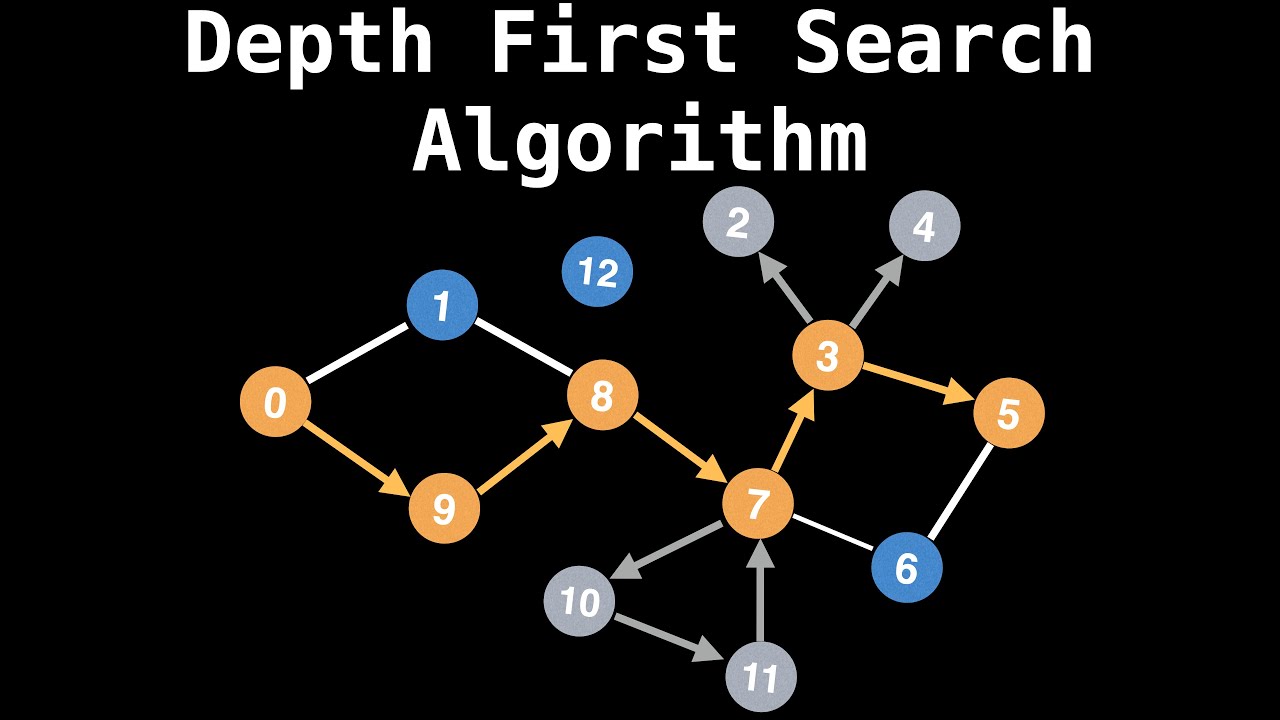
Graph Theory in AI
Graph theory provides tools to represent and analyze relationships between entities in AI. Algorithms like breadth-first search and depth-first search are used to traverse and explore graphs. Graph theory is applied in various AI applications such as social network analysis and recommendation systems.	Image Source
		5

Optimization in AI
Optimization is at the core of AI, enabling the selection of the best solutions from a set of possibilities. Techniques like linear programming, integer programming, and evolutionary algorithms are used to solve optimization problems in AI. Optimization algorithms help in training models, finding optimal paths, and resource allocation in AI systems.	Image Source
		6

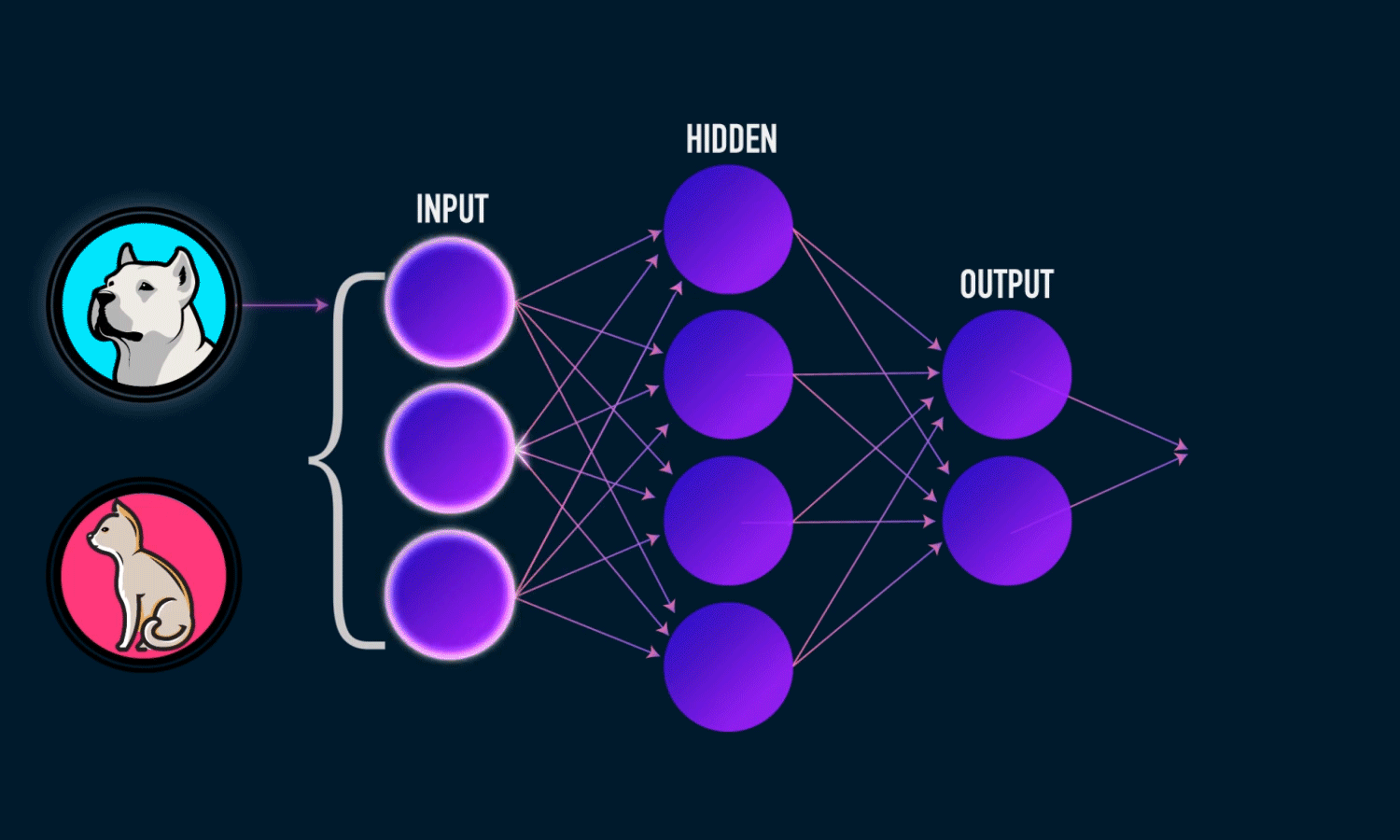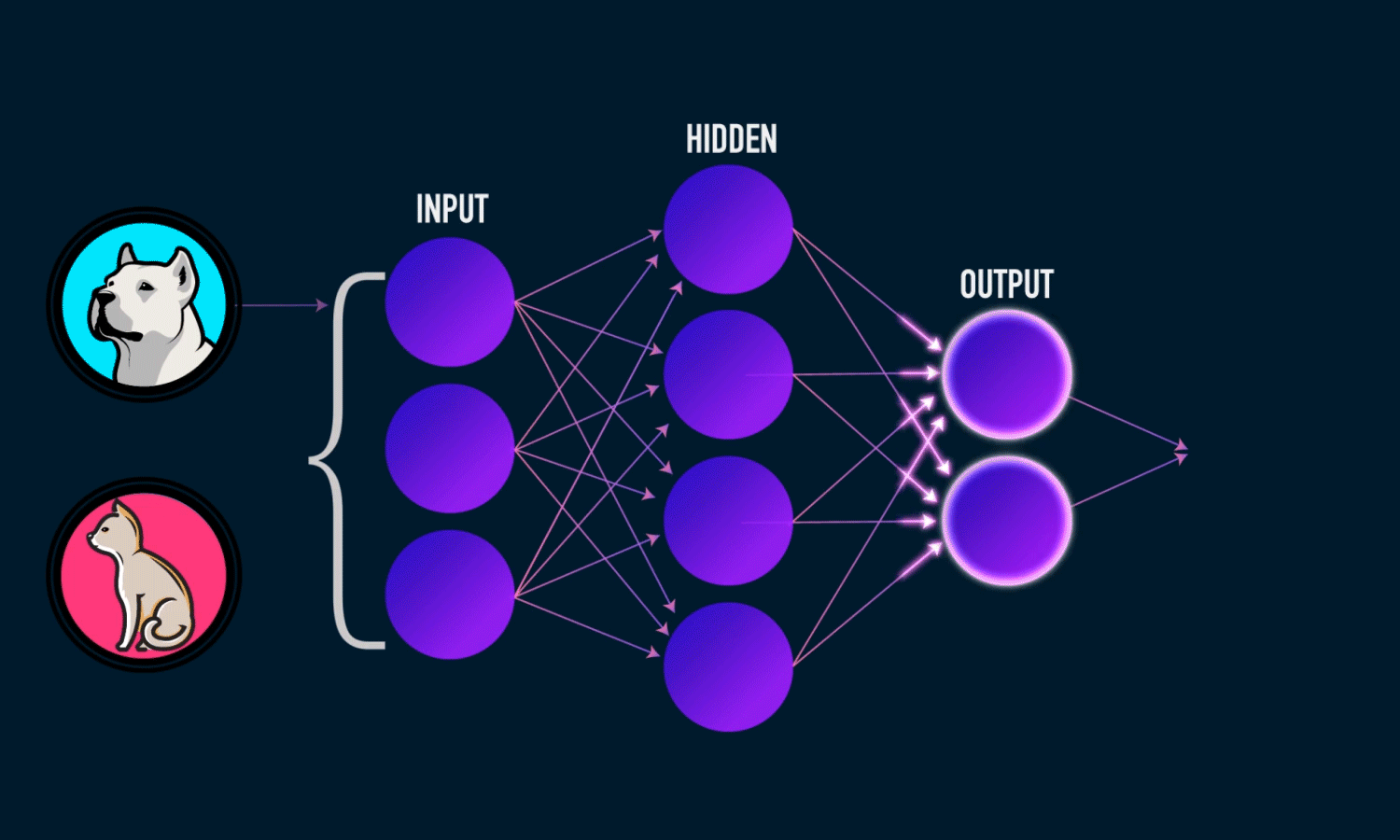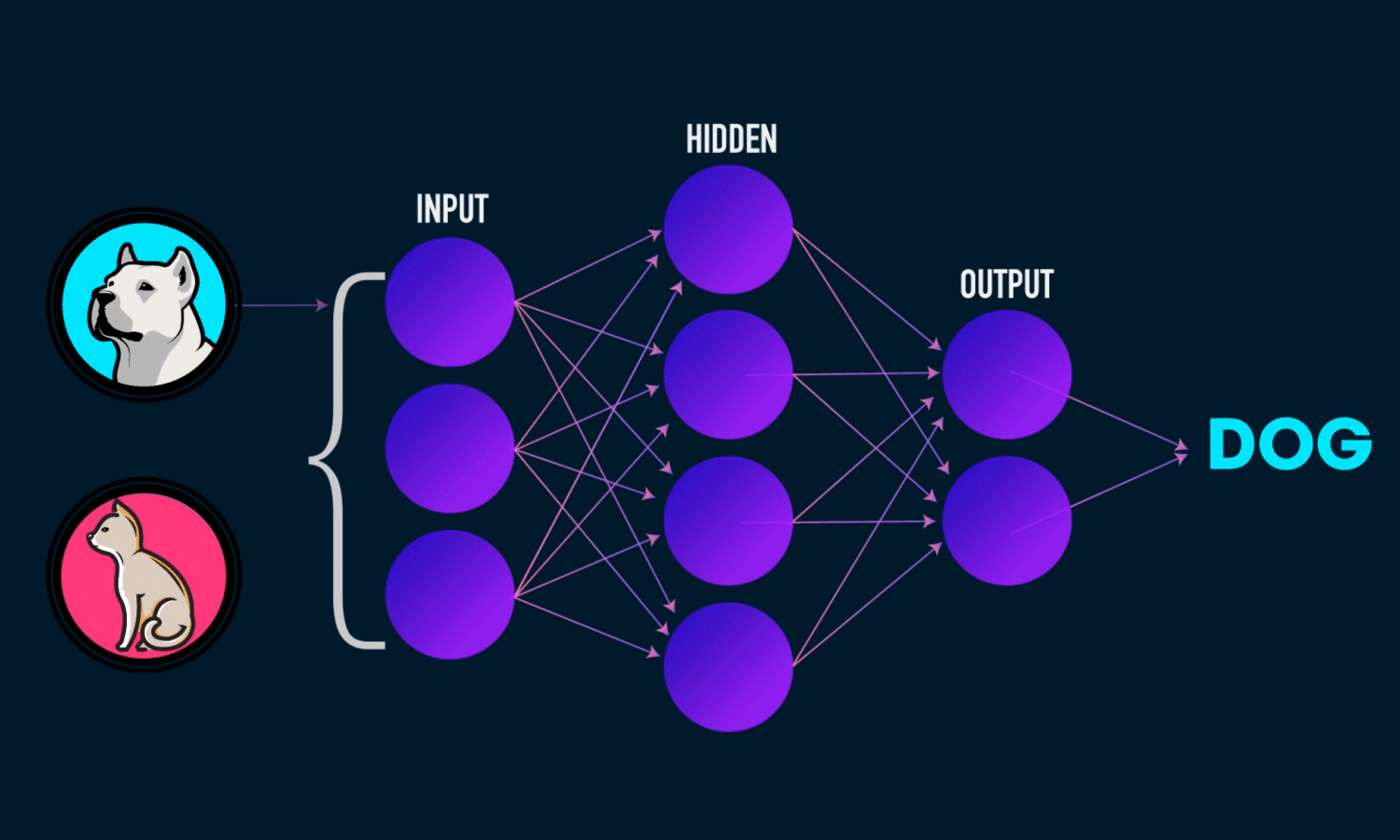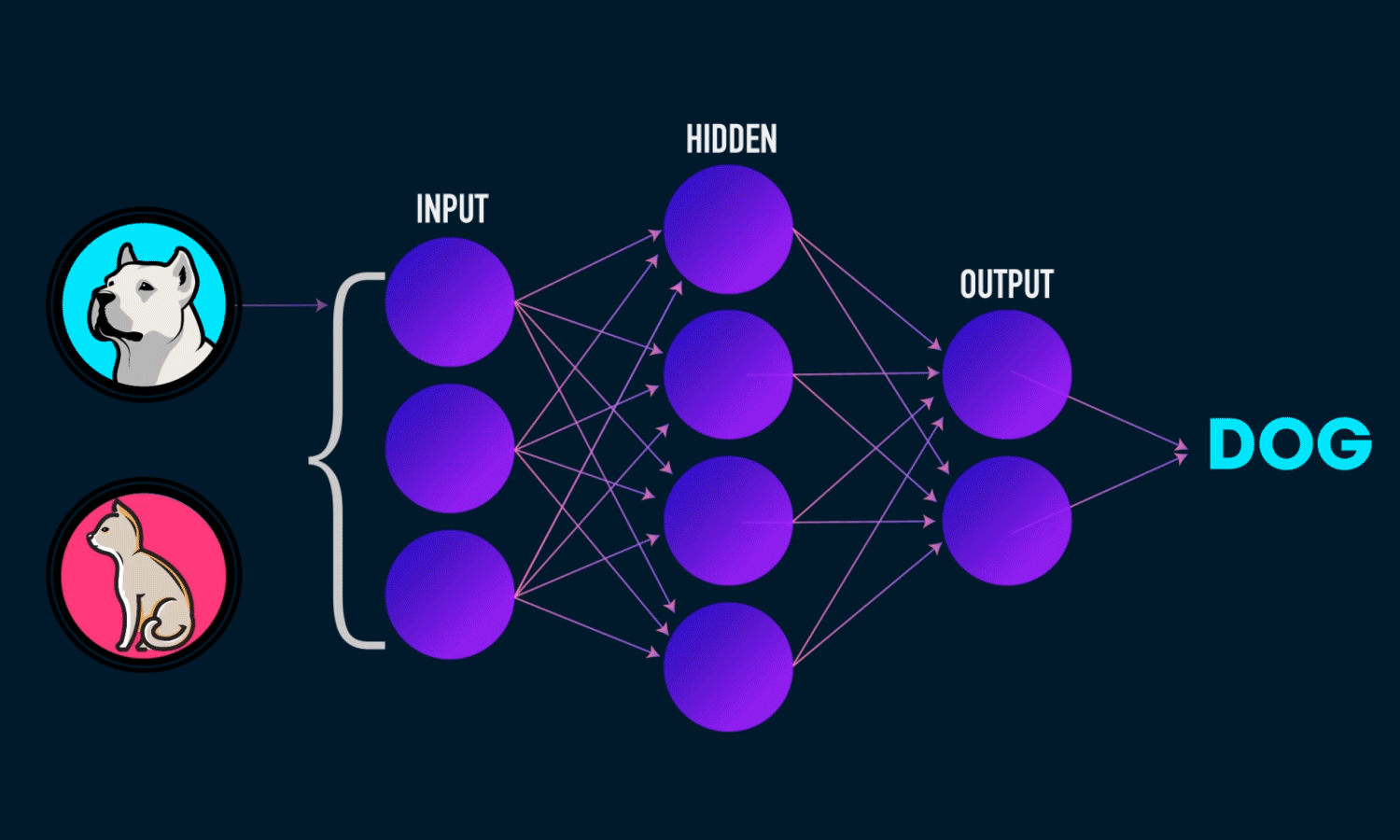
Neural Networks and Deep Learning
Neural networks, inspired by the structure of the human brain, are used to solve complex problems in AI. The mathematics behind neural networks involves linear algebra, calculus, and optimization techniques. Deep learning, a subset of neural networks, uses multiple layers to extract hierarchical representations from data.	Image Source
		7

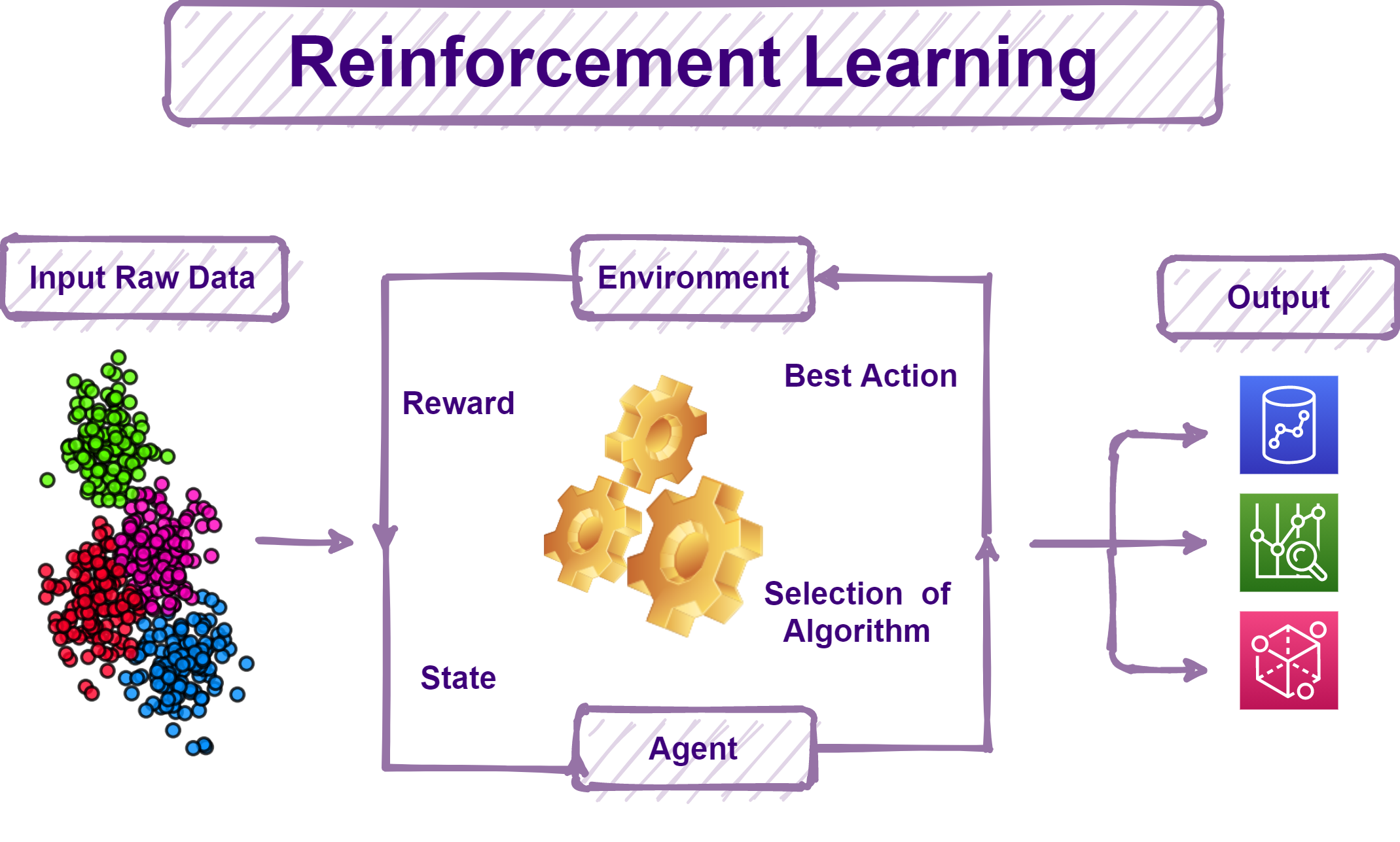
Reinforcement Learning
Reinforcement learning is a branch of AI where an agent learns through interaction with an environment. Mathematics, particularly Markov decision processes, are used to model and solve reinforcement learning problems. Reinforcement learning algorithms aim to maximize a reward signal by learning optimal policies.	Image Source
		8

Natural Language Processing (NLP)
NLP involves the interaction between computers and human language, enabling machines to understand and generate text. Mathematics helps in language modeling, sentiment analysis, and machine translation in NLP. Techniques like probabilistic models, hidden Markov models, and word embeddings are applied in NLP algorithms.	Image Source
		9

Conclusion
Mathematics provides the foundation for various aspects of AI, including machine learning, optimization, and natural language processing. Understanding mathematical concepts and algorithms is crucial for developing and improving AI systems. Continual advancements in both mathematics and AI will further enhance the capabilities of artificial intelligence.	Image Source
		10

References (download PPTX file for details)
Goodfellow, I., Bengio, Y., & Courville, A. (... Murphy, K. P. (2012). Machine learning: a pro... Russell, S., & Norvig, P. (2016). Artificial ...
		11

Join the SlideMake Community