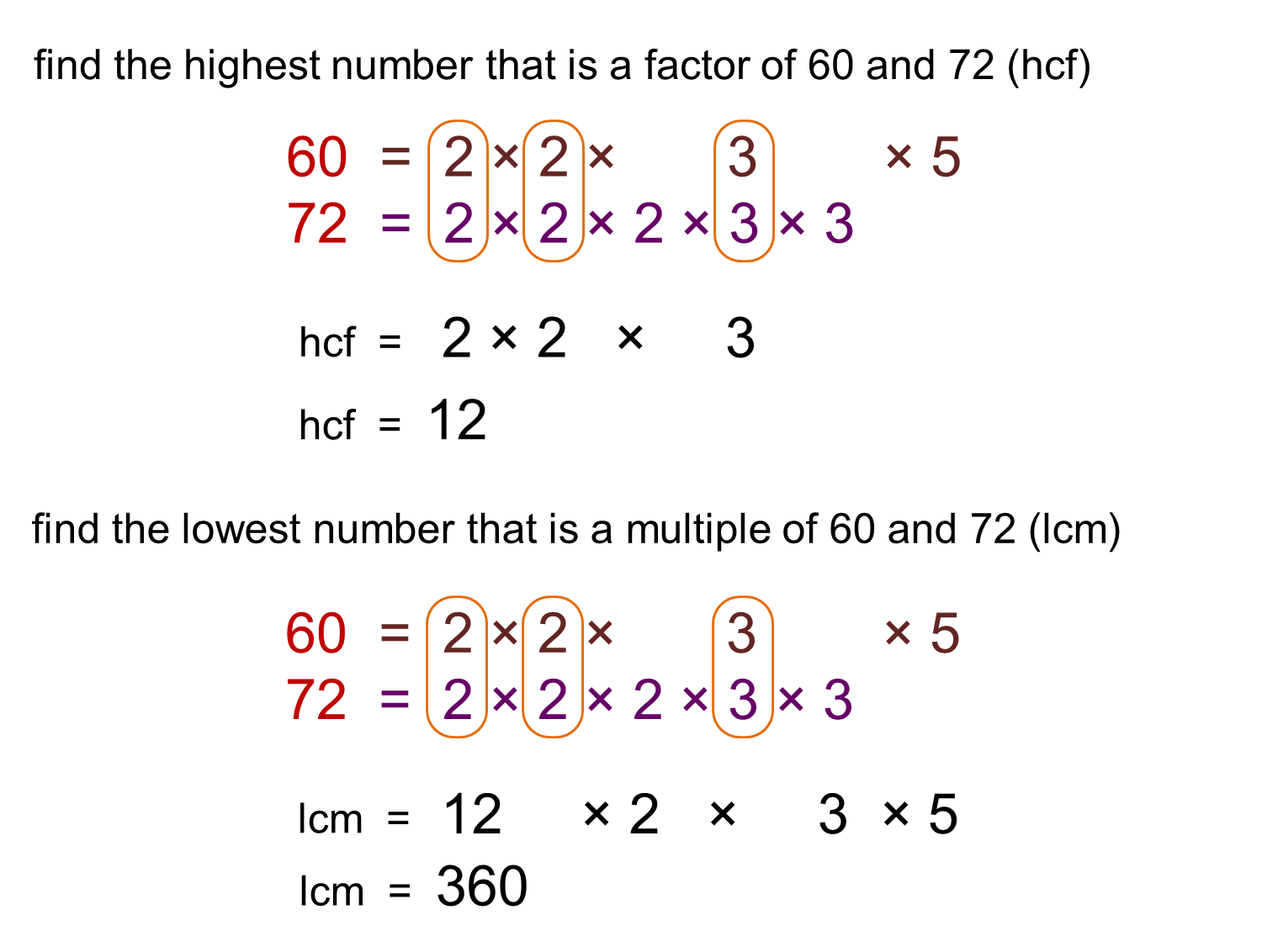LCM & HCF Presentation
| Introduction to LCM & HCF | ||
|---|---|---|
| LCM stands for Least Common Multiple, and HCF stands for Highest Common Factor. LCM is the smallest multiple that two or more numbers have in common. HCF is the largest factor that two or more numbers have in common. | ||
| 1 | ||
| LCM Calculation | ||
|---|---|---|
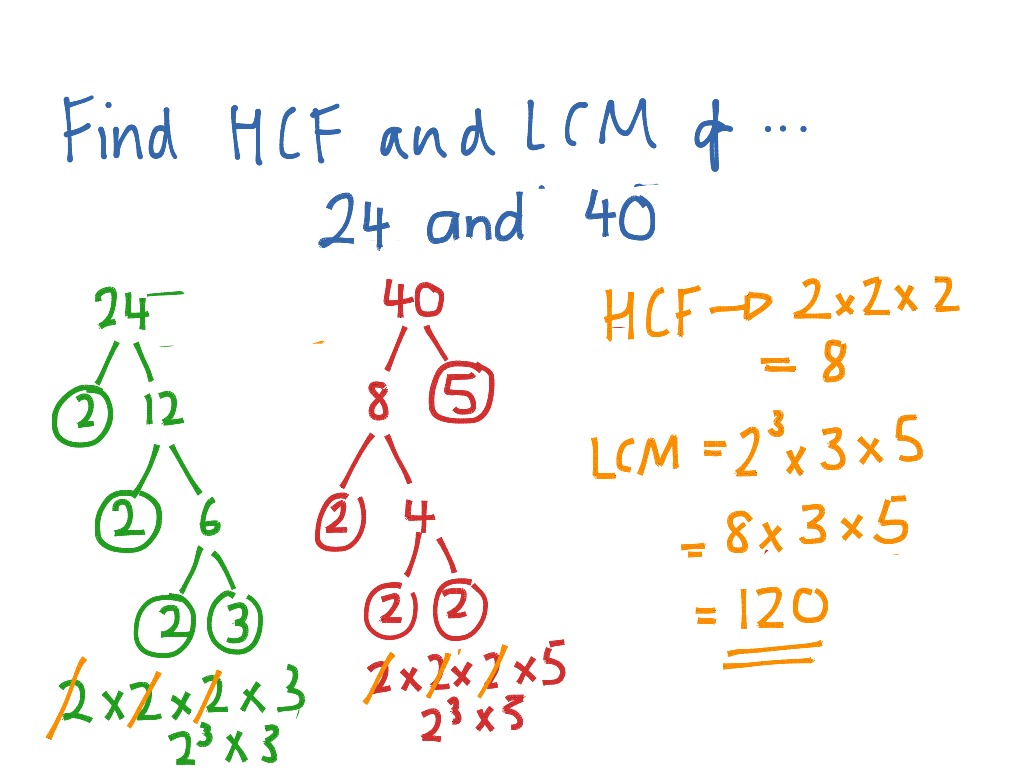
| To find the LCM, list the multiples of each number until you find a common multiple. Alternatively, you can use the prime factorization method to find the LCM. LCM is essential for solving problems involving fractions, ratios, and proportions. | ||
| 2 | ||
| HCF Calculation | ||
|---|---|---|
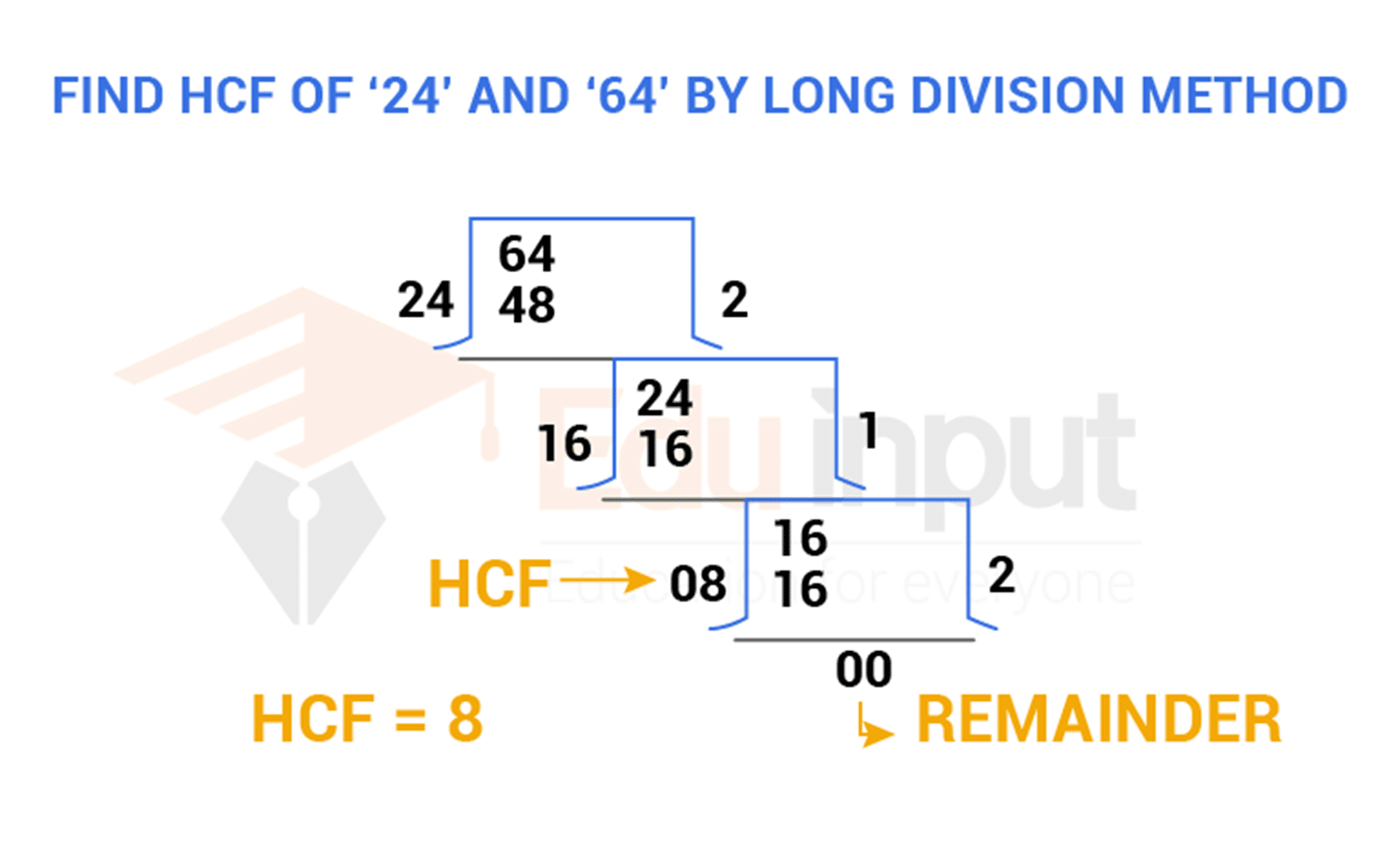
| To find the HCF, list the factors of each number and find the largest factor they have in common. Alternatively, you can use the prime factorization method to find the HCF. HCF is useful in simplifying fractions and finding the greatest common divisor of two or more numbers. | ||
| 3 | ||
| LCM & HCF Relationship | ||
|---|---|---|
| LCM and HCF are two different concepts but are related to each other. The product of LCM and HCF of two numbers is equal to the product of the two numbers. LCM and HCF are complementary operations in number theory. | ||
| 4 | ||
| Applications of LCM & HCF | ||
|---|---|---|
| LCM is used in scheduling tasks, finding the next meeting time, and calculating time intervals. HCF is used in simplifying fractions, dividing resources equally, and solving problems involving sharing or distribution. Both LCM and HCF find applications in various fields like mathematics, computer science, engineering, and finance. | ||
| 5 | ||
| LCM & HCF Examples | ||
|---|---|---|
| Example 1: Find the LCM and HCF of 12 and 18.
- LCM: Multiples of 12: 12, 24, 36, 48, ... | Multiples of 18: 18, 36, 54, ...
- LCM: 36 is the smallest common multiple.
- HCF: Factors of 12: 1, 2, 3, 4, 6, 12 | Factors of 18: 1, 2, 3, 6, 9, 18
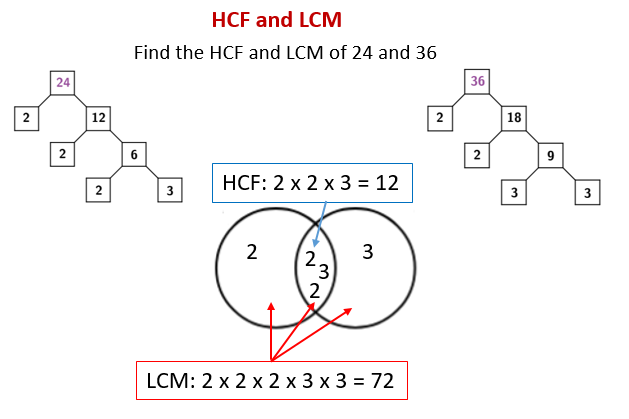
- HCF: 6 is the largest common factor. Example 2: Find the LCM and HCF of 24 and 36 using prime factorization. - LCM: Prime factors of 24: 2 x 2 x 2 x 3 | Prime factors of 36: 2 x 2 x 3 x 3 - LCM: Multiply the highest power of each prime factor: 2 x 2 x 2 x 3 x 3 = 72 - HCF: Prime factors of 24: 2 x 2 x 2 x 3 | Prime factors of 36: 2 x 2 x 3 x 3 - HCF: Multiply the common prime factors: 2 x 2 x 3 = 12 Your third bullet |  | |
| 6 | ||
| LCM & HCF in Real Life | ||
|---|---|---|
| LCM: In a bakery, determining when multiple batches of bread will be ready simultaneously. HCF: In a classroom, dividing a set number of books equally among a group of students. LCM: In a construction project, calculating when multiple workers will finish at the same time. | ||
| 7 | ||
| Tips for LCM & HCF Calculation | ||
|---|---|---|
| Use prime factorization for larger numbers to simplify calculations. Practice listing multiples and factors regularly to improve speed and accuracy. Understand the relationship between LCM and HCF to solve complex problems efficiently. | ||
| 8 | ||
| Common Mistakes to Avoid | ||
|---|---|---|
| Forgetting to check if the numbers have any common factors before calculating LCM or HCF. Only focusing on one method of calculation without considering alternate approaches. Relying solely on calculators or technology without understanding the underlying concepts. | ||
| 9 | ||
| Conclusion | ||
|---|---|---|
| LCM and HCF are fundamental concepts in mathematics. LCM helps find the smallest common multiple, while HCF helps find the largest common factor. Understanding and applying LCM and HCF are essential in various fields and real-life situations. | ||
| 10 | ||
| References (download PPTX file for details) | ||
|---|---|---|
| Mathisfun.com: Least Common Multiple... Mathisfun.com: Highest Common Factor... Khan Academy: LCM and GCF... |  | |
| 11 | ||