Heisenberg's Uncertainty Principle And Borns Equation Presentation

Heisenberg's Uncertainty Principle
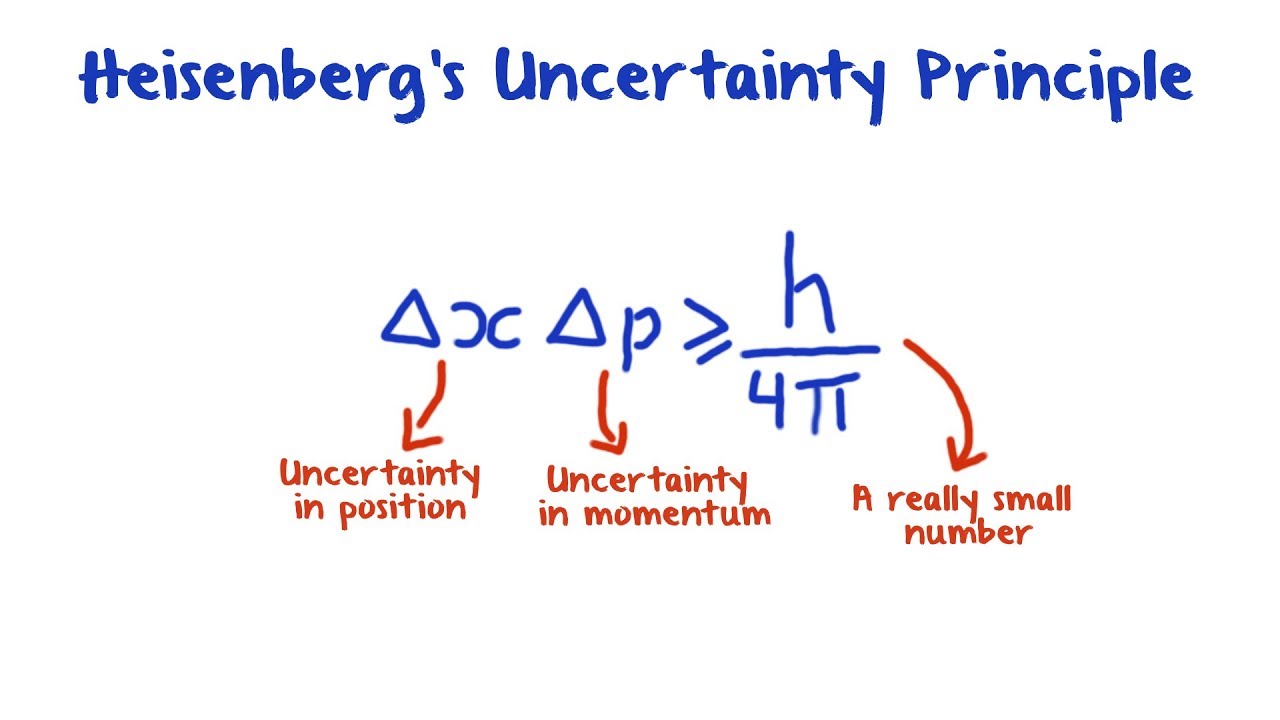
Heisenberg's Uncertainty Principle is a fundamental concept in quantum mechanics. It states that it is impossible to simultaneously know the exact position and momentum of a particle with absolute certainty. This principle introduces a fundamental limit to the precision with which certain pairs of physical properties of a particle can be measured.	Image Source
		1

Uncertainty in Position
According to Heisenberg's Uncertainty Principle, the more precisely we try to measure the position of a particle, the less precisely we can know its momentum. This means that the more accurately we determine the location of a particle, the more uncertain we become about its speed or direction of motion. The uncertainty in position is related to the wavelength of the particle's wave function.	Image Source
		2

Uncertainty in Momentum
Similarly, the more precisely we try to measure the momentum of a particle, the less precisely we can know its position. This implies that the more accurately we determine the momentum of a particle, the more uncertain we become about its position. The uncertainty in momentum is related to the spatial extent of the particle's wave function.	Image Source
		3

Mathematical Formulation
Heisenberg's Uncertainty Principle is mathematically represented as ∆x ∆p ≥ h/ 4π, where ∆x represents the uncertainty in position, ∆p represents the uncertainty in momentum, and h is the reduced Planck's constant. This equation states that the product of the uncertainties in position and momentum must be greater than or equal to a minimum value. The uncertainty principle emphasizes the inherent probabilistic nature of quantum mechanics.	Image Source
		4

Born's Equation
Born's equation, formulated by Max Born, provides a way to interpret the wave function in quantum mechanics. The equation relates the wave function Ψ and the probability density function ρ. Born's equation is given as ρ = Ψ	Image Source
		5

Probability Interpretation
Born's equation allows us to interpret the square of the wave function, |Ψ|^2, as the probability density of finding a particle at a specific location in space. The probability density ρ gives the likelihood of finding the particle in a small volume element at a particular position. This interpretation aligns with experimental observations and provides a connection between the mathematical formalism of quantum mechanics and observable quantities.
		6

Wave-Particle Duality
Heisenberg's Uncertainty Principle and Born's equation are closely related to the wave-particle duality of quantum mechanics. They highlight that particles, such as electrons and photons, can exhibit both wave-like and particle-like properties. This duality is a fundamental aspect of the quantum world and challenges our classical intuition about the behavior of physical entities.	Image Source
		7

Practical Implications
Heisenberg's Uncertainty Principle and Born's equation have profound implications for various areas of physics, such as quantum mechanics, atomic physics, and particle physics. They provide a framework for understanding the limits of measurement precision and the probabilistic nature of quantum systems. These principles have played a crucial role in the development of modern physics and technologies, including quantum computing and cryptography.	Image Source
		8

Summary
Heisenberg's Uncertainty Principle states that there are inherent limits to the precision with which certain pairs of physical properties of a particle can be measured simultaneously. Born's equation connects the wave function to the probability density, allowing us to interpret the square of the wave function as the probability of finding a particle at a specific location. These principles underpin the probabilistic nature of quantum mechanics and the wave-particle duality exhibited by particles.
		9

References (download PPTX file for details)
Bohr, N. (1928). The quantum postulate and th... Griffiths, D. J. (2005). Introduction to Quan... Shankar, R. (1994). Principles of Quantum Mec...
		10