Fourier Transform Of Standard Signals, Fourier Transform Of Periodic Signals Presentation

Introduction to Fourier Transform
The Fourier Transform is a mathematical tool used to analyze the frequency components of a signal. It transforms a signal from the time domain to the frequency domain. The Fourier Transform can be used to decompose a signal into its constituent frequencies.	Image Source
		1

Fourier Transform of Standard Signals
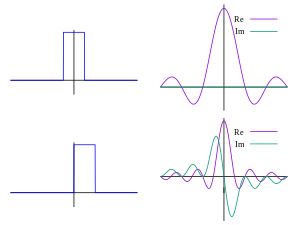
Standard signals are commonly used to analyze the properties of the Fourier Transform. Examples of standard signals include impulse, step, and sinusoidal signals. The Fourier Transform of an impulse signal is a constant value across all frequencies.	Image Source
		2

Fourier Transform of Standard Signals (Continued)
The Fourier Transform of a step signal results in a sinc function in the frequency domain. The Fourier Transform of a sinusoidal signal consists of two delta functions at positive and negative frequencies. Your third bullet	Image Source
		3

Fourier Transform of Periodic Signals
Periodic signals are signals that repeat themselves after a certain period. The Fourier Transform of a periodic signal results in a discrete spectrum in the frequency domain. The discrete spectrum consists of a series of harmonics at multiples of the fundamental frequency.	Image Source
		4

Fourier Transform of Periodic Signals (Continued)
The Fourier Transform of a periodic square wave results in a series of odd harmonics. The amplitude of each harmonic decreases as the frequency increases. The Fourier Transform of a periodic triangle wave results in a series of odd and even harmonics.	Image Source
		5

Conclusion
The Fourier Transform is a powerful tool for analyzing the frequency components of signals. It can be used to decompose signals into their constituent frequencies. Understanding the Fourier Transform of standard and periodic signals is essential in signal processing and communication systems.	Image Source
		6

Join the SlideMake Community