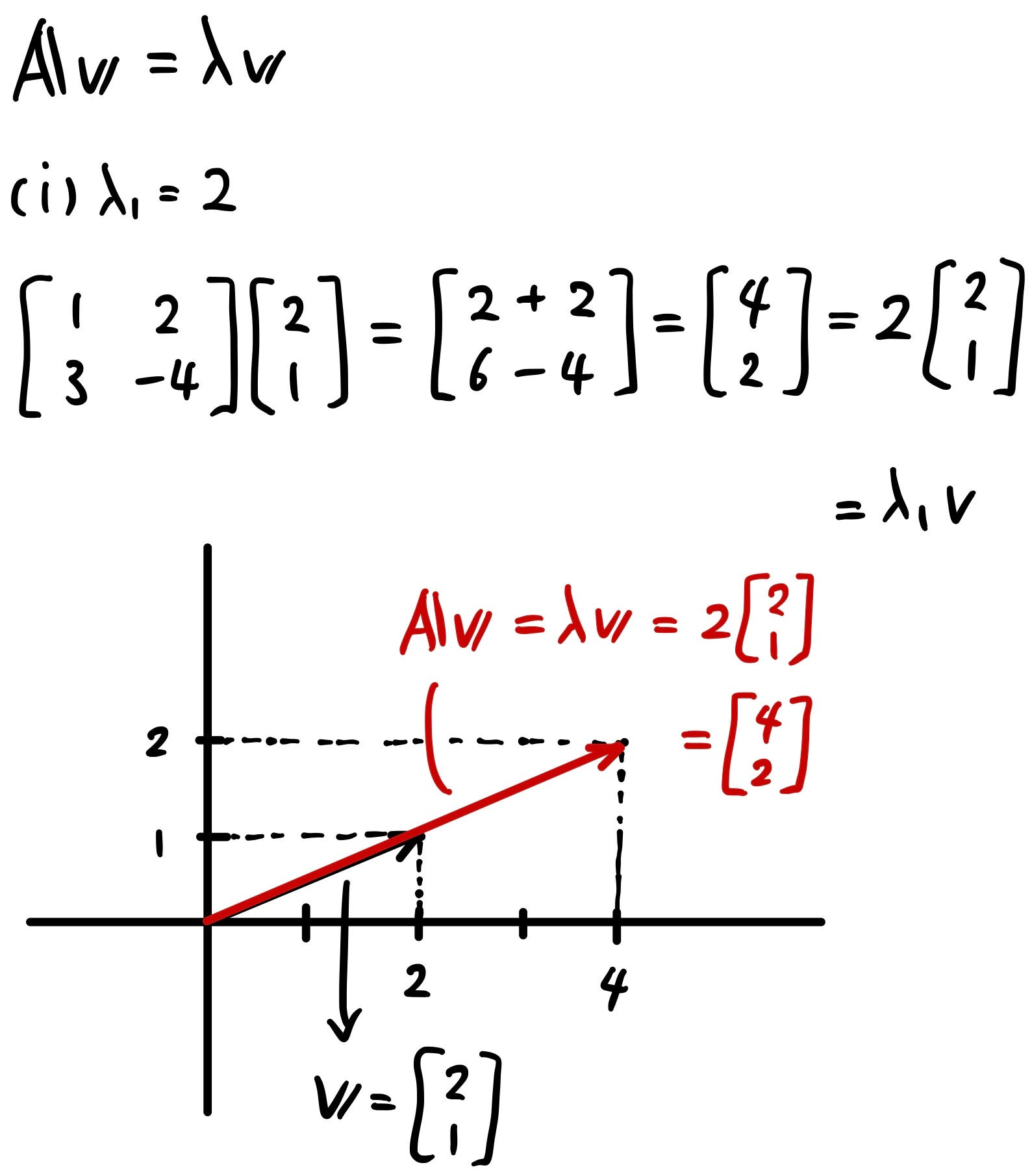Eigen Vectors And Eigen Values Presentation

Introduction to Eigen vectors and Eigen values.
Eigen vectors and eigen values are fundamental concepts in linear algebra. Eigen vectors are non-zero vectors that only change by a scalar factor when a linear transformation is applied. Eigen values are the scalars that represent the amount of stretching or compression of the corresponding eigen vectors.	Image Source
		1

Eigenvectors and Eigenvalues in 2D.
In 2D, eigen vectors can be visualized as axes that remain in the same direction but may change in length. Eigen values in 2D represent the scaling factor along the corresponding eigen vectors. Eigenvectors are orthogonal to each other.	Image Source
		2

Eigenvectors and Eigenvalues in 3D.
In 3D, eigen vectors can be visualized as planes that remain unchanged or change only by scaling. Eigen values in 3D represent the scaling factor along the corresponding eigen vectors. Eigenvectors are orthogonal to each other.	Image Source
		3

Calculation of Eigenvalues and Eigenvectors.
Eigenvalues and eigenvectors can be calculated by solving the characteristic equation: det(A - λI) = 0, where A is the matrix and λ is the eigenvalue. Once eigenvalues are found, eigenvectors can be obtained by solving the equation (A - λI)v = 0, where v is the eigenvector. Eigenvectors can also be found by row reducing the matrix (A - λI) to its reduced row-echelon form.	Image Source
		4

Applications of Eigenvalues and Eigenvectors.
Eigenvalues and eigenvectors are widely used in image processing techniques like image compression and denoising. They are used in principal component analysis (PCA) for dimensionality reduction and pattern recognition. Eigenvalues and eigenvectors play a crucial role in solving differential equations and analyzing dynamic systems.	Image Source
		5

Diagonalization of Matrices.
Diagonalization of a matrix involves expressing it in terms of its eigenvalues and eigenvectors. A matrix A can be diagonalized as A = PDP^(-1), where D is a diagonal matrix containing eigenvalues and P is a matrix with corresponding eigenvectors as columns. Diagonalization simplifies matrix calculations and makes certain operations easier.	Image Source
		6

Properties of Eigenvalues and Eigenvectors.
Eigenvalues are always real for real symmetric matrices. Eigenvectors corresponding to distinct eigenvalues are linearly independent. The sum of eigenvalues equals the trace of the matrix, and the product of eigenvalues equals the determinant of the matrix.	Image Source
		7

Complex Eigenvalues and Eigenvectors.
Complex eigenvalues and eigenvectors arise when dealing with non-symmetric matrices. Complex eigenvalues always occur in conjugate pairs. Eigenvectors corresponding to complex eigenvalues are also complex conjugates of each other.	Image Source
		8

Eigenvalues and Eigenvectors in Machine Learning.
Eigenvalues and eigenvectors are utilized in dimensionality reduction techniques like Singular Value Decomposition (SVD). They help in finding important features and reducing noise in data. Eigenvalues can be used to determine the condition number of a matrix, which indicates its stability and sensitivity to perturbations.	Image Source
		9

Summary and Conclusion.
Eigenvalues and eigenvectors are essential concepts in linear algebra with various applications in mathematics, physics, and computer science. They provide insights into the geometric and algebraic properties of matrices. Understanding eigenvalues and eigenvectors helps in solving problems efficiently and analyzing complex systems.	Image Source
		10

References (download PPTX file for details)
Gilbert Strang. Introduction to Linear Algebr... Jim Hefferon. Linear Algebra, 4th Edition. Or... Stephen Boyd and Lieven Vandenberghe. Convex ...
		11

Join the SlideMake Community