Divergence Theorem Presentation
| Introduction to Divergence Theorem | ||
|---|---|---|
| The Divergence Theorem is a fundamental theorem in vector calculus. It relates the flow of a vector field across a closed surface to the divergence of the vector field within the volume enclosed by the surface. The theorem is also known as Gauss's theorem or Gauss's divergence theorem. | ||
| 1 | ||
| Statement of Divergence Theorem | ||
|---|---|---|
| The Divergence Theorem states that the flux of a vector field F through a closed surface S is equal to the triple integral of the divergence of F over the volume V enclosed by S. Mathematically, it can be written as ∬S F · dA = ∭V ∇ · F dV. Here, ∬S represents the surface integral, ∭V represents the volume integral, F is the vector field, dA is the area vector, and ∇ · F is the divergence of F. | ||
| 2 | ||
| Physical Interpretation | ||
|---|---|---|
| The Divergence Theorem allows us to relate the behavior of a vector field on the surface to its behavior within the enclosed volume. It provides a powerful tool for understanding fluid flow, electric and magnetic fields, and other phenomena in physics. The flux of a vector field through a closed surface can be calculated by evaluating the divergence of the vector field within the enclosed volume. | ||
| 3 | ||
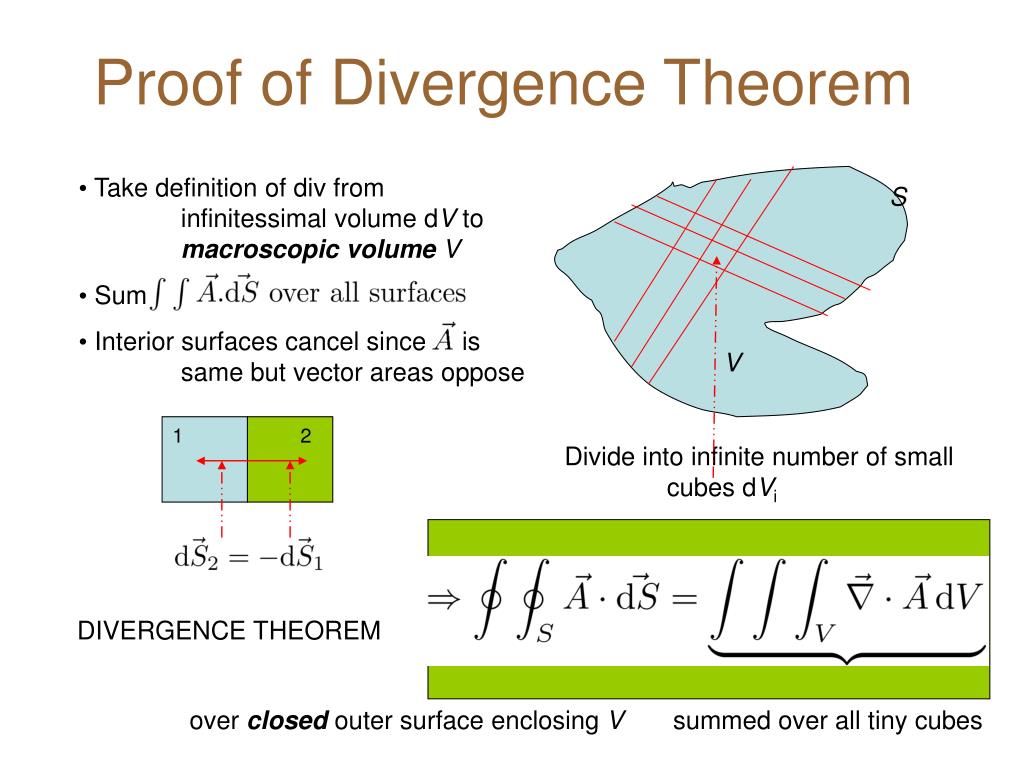
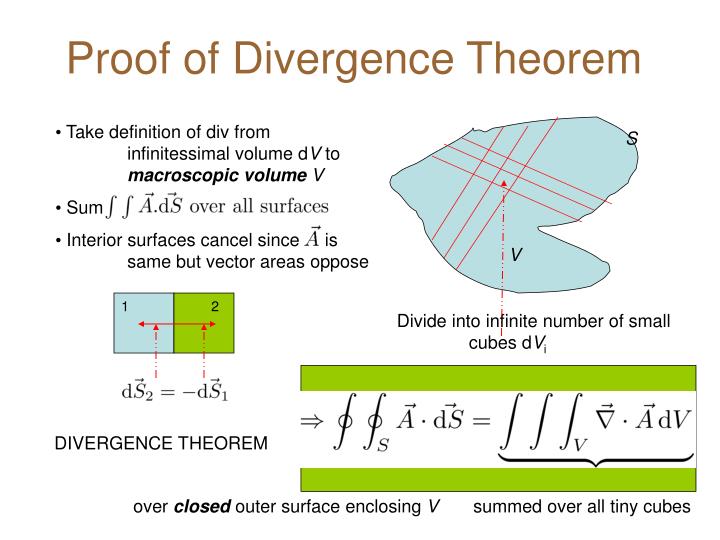
| Proof of Divergence Theorem | ||
|---|---|---|
| The proof of the Divergence Theorem involves splitting the closed surface S into infinitesimally small surface elements. The flux through each small surface element is related to the divergence of the vector field at that point. By summing up the flux through all the surface elements and taking the limit as the size of the elements approaches zero, we obtain the integral form of the Divergence Theorem. | ||
| 4 | ||
| Applications in Physics - Fluid Flow | ||
|---|---|---|
| The Divergence Theorem is extensively used in fluid dynamics to analyze the flow of fluids through surfaces. It allows us to calculate the net flow of a fluid through a closed surface by evaluating the divergence of the velocity field. This is crucial in studying fluid dynamics, from understanding the behavior of water flow to designing efficient pipelines. | ||
| 5 | ||
| Applications in Physics - Electrostatics | ||
|---|---|---|
| In electrostatics, the Divergence Theorem is used to relate the electric field to the charge distribution within a closed surface. It allows us to calculate the total electric flux through a closed surface by evaluating the divergence of the electric field. This is fundamental in understanding electric fields, calculating electric potential, and analyzing charge distributions. | ||
| 6 | ||
| Applications in Physics - Magnetism | ||
|---|---|---|
| Similarly, in magnetism, the Divergence Theorem is used to relate the magnetic field to the current distribution within a closed surface. It allows us to calculate the total magnetic flux through a closed surface by evaluating the divergence of the magnetic field. This is important in understanding magnetic fields, analyzing magnetic materials, and designing magnetic devices. | ||
| 7 | ||
| Relationship with Other Theorems | ||
|---|---|---|
| The Divergence Theorem is closely related to other fundamental theorems in vector calculus, such as Stokes' theorem and Green's theorem. Stokes' theorem relates the circulation of a vector field along a closed curve to the curl of the vector field within the surface bounded by the curve. Green's theorem relates the circulation of a vector field along a closed curve to the flux of the curl of the vector field through a surface bounded by the curve. | ||
| 8 | ||
| Conclusion | ||
|---|---|---|
| The Divergence Theorem is a powerful tool in vector calculus that relates the flow of a vector field through a closed surface to the divergence of the vector field within the enclosed volume. It finds applications in various fields of physics, including fluid dynamics, electrostatics, and magnetism. Understanding and applying the Divergence Theorem is essential for analyzing and solving problems involving vector fields in physics and engineering. | ||
| 9 | ||