DE BROGLIE HYPOTHESIS Presentation

Introduction to the De Broglie Hypothesis
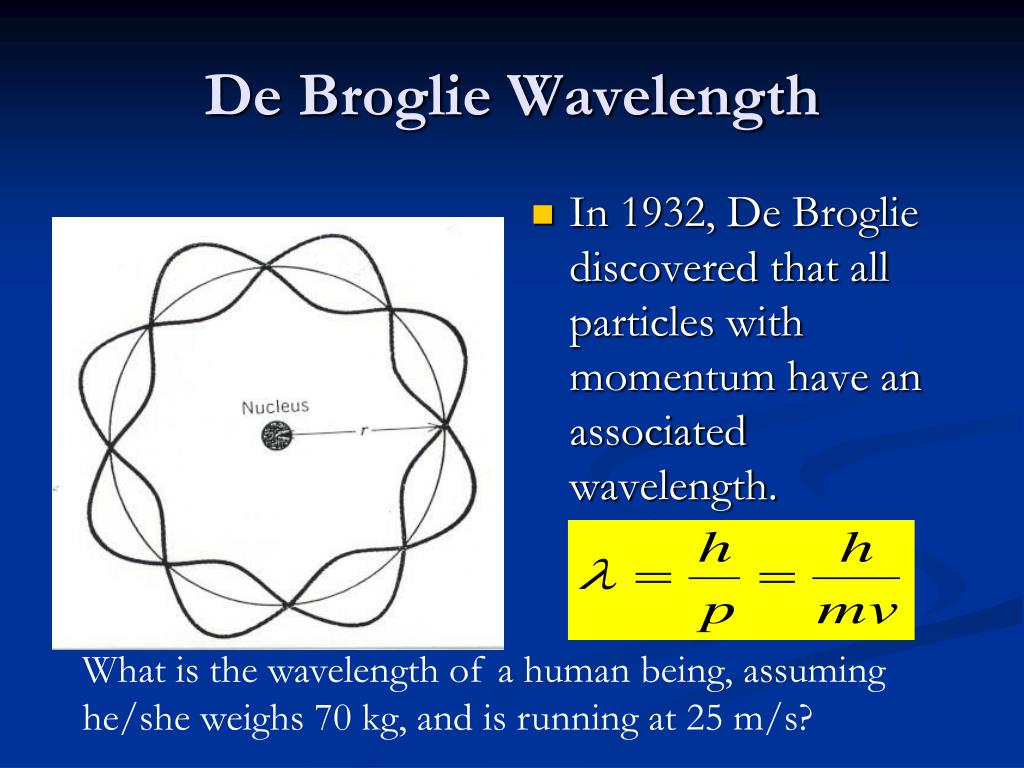
The De Broglie Hypothesis states that particles, such as electrons, have wave-like properties. Proposed by Louis de Broglie in 1924, it extends the wave-particle duality concept of quantum mechanics. According to the hypothesis, every particle with momentum has an associated wavelength.	Image Source
		1

Particle-Wave Duality
The wave-particle duality concept suggests that particles can exhibit both wave and particle-like behavior. De Broglie's hypothesis built upon this idea by proposing that particles also have wave properties. It implies that particles can interfere with each other, just like waves do.	Image Source
		2

Equation for De Broglie Wavelength
The De Broglie wavelength (λ) of a particle is given by the equation: λ = h / p λ represents the wavelength, h is Planck's constant, and p denotes the momentum of the particle. The equation shows that the wavelength decreases as the momentum of the particle increases.	Image Source
		3

Experimental Confirmation
The De Broglie Hypothesis was experimentally confirmed by Davisson and Germer in 1927. They observed electron diffraction, which is the bending of electron beams in a crystal lattice. This diffraction pattern supported the wave-like nature of electrons proposed by de Broglie.	Image Source
		4

Applications of De Broglie Hypothesis
The De Broglie Hypothesis is fundamental to understanding quantum mechanics. It explains phenomena such as electron diffraction, which is used in electron microscopy. The hypothesis also plays a crucial role in particle accelerators and quantum computing.	Image Source
		5

Relation to Heisenberg's Uncertainty Principle
De Broglie's hypothesis is closely related to Heisenberg's Uncertainty Principle. The Uncertainty Principle states that the position and momentum of a particle cannot be precisely determined simultaneously. De Broglie's wavelength provides a connection between the uncertainty in momentum and the spatial extent of the wave function.	Image Source
		6

Limitations of De Broglie Hypothesis
The De Broglie Hypothesis is valid for particles with non-relativistic velocities. It fails to accurately describe the behavior of particles traveling at relativistic speeds. For relativistic particles, the more comprehensive theory of quantum field theory is used.	Image Source
		7

Significance in Modern Physics
The De Broglie Hypothesis paved the way for the development of quantum mechanics. It provided a crucial understanding of the wave-particle duality of matter. The hypothesis revolutionized our understanding of the behavior of particles at the atomic and subatomic levels.	Image Source
		8

De Broglie's Contribution to Science
De Broglie's work on the wave-particle duality earned him the Nobel Prize in Physics in 1929. His hypothesis was a significant step towards the development of quantum mechanics. De Broglie's groundbreaking ideas continue to shape our understanding of the microscopic world.	Image Source
		9

References (download PPTX file for details)
Davisson, C., & Germer, L. H. (1927). Diffrac... De Broglie, L. (1925). Recherches sur la théo... Griffiths, D. J. (2005). Introduction to quan...
		10

References (download PPTX file for details)
Your first bullet... Your second bullet... Your third bullet...
		11

Join the SlideMake Community