Applications Of Integral Calculus Presentation

Introduction to Applications of Integral Calculus
Integral calculus is a branch of mathematics that deals with the concept of integration. It has numerous practical applications in various fields, including physics, engineering, economics, and biology. By understanding the applications of integral calculus, we can solve real-world problems and make accurate predictions.	Image Source
		1

Area and Volume Calculation
One of the primary applications of integral calculus is calculating the area under a curve. It helps us find the area of irregular shapes and curved surfaces. Additionally, integral calculus allows us to calculate the volume of three-dimensional objects, such as solids of revolution.	Image Source
		2

Physics and Engineering
Integral calculus is extensively used in physics and engineering to analyze motion, forces, and energy. It enables us to determine displacement, velocity, and acceleration by integrating the equations of motion. In engineering, integral calculus helps in designing structures, calculating fluid flow, and optimizing systems.	Image Source
		3

Economics and Business
Integral calculus plays a crucial role in economics and business analysis. It aids in understanding the concepts of supply and demand, marginal cost, and revenue. By using integrals, we can evaluate total profit, consumer surplus, and producer surplus.	Image Source
		4

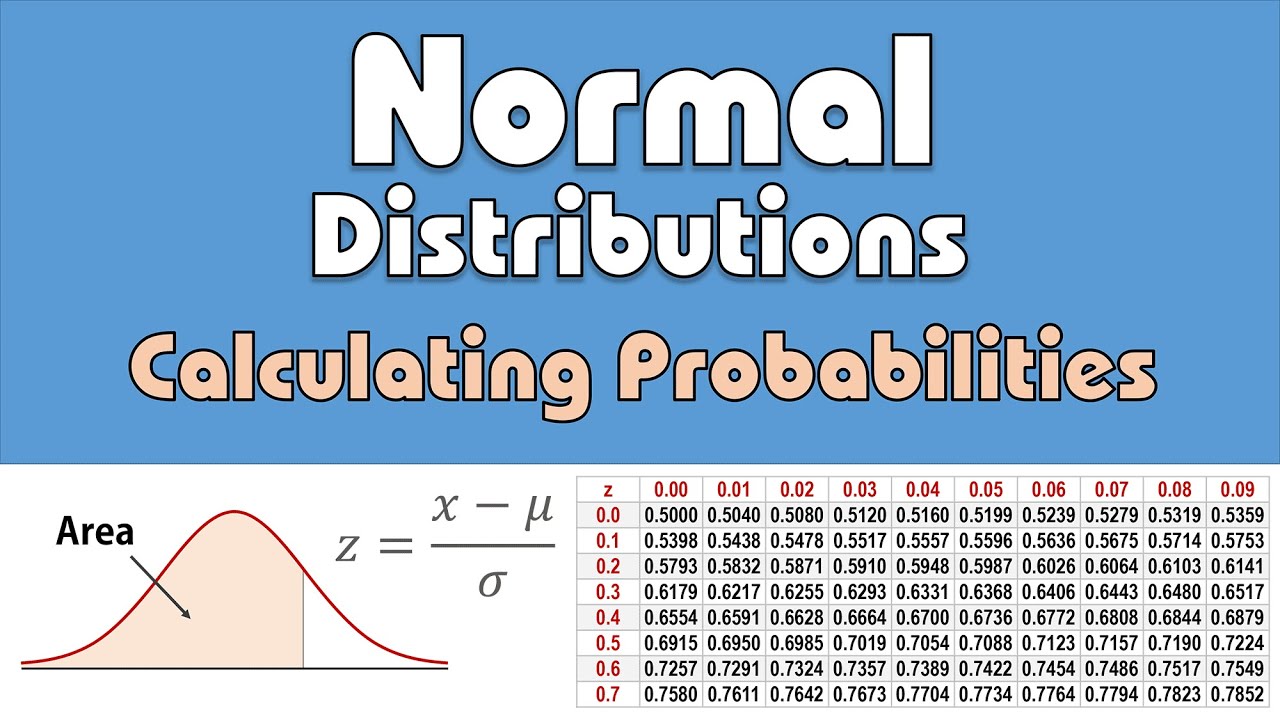
Probability and Statistics
In probability theory, integral calculus is used to calculate probabilities and expected values. It helps in determining the cumulative distribution function and probability density function. In statistics, integral calculus is involved in finding the area under probability density functions to calculate probabilities.	Image Source
		5

Optimization Problems
Integral calculus plays a significant role in solving optimization problems. It helps in finding the maximum or minimum of a function by analyzing its derivative and integrating it. Optimization problems can be found in various fields, including engineering, economics, and physics.	Image Source
		6

Biological Applications
In biology, integral calculus is used to model population growth and decay. It helps in understanding the dynamics of ecosystems and the spread of diseases. Integral calculus is also used to calculate drug concentrations in the body over time.	Image Source
		7

Signal Processing and Image Analysis
In signal processing, integral calculus is involved in analyzing and processing continuous signals. It helps in calculating the area under the curve of the signal, determining signal power, and filtering unwanted noise. In image analysis, integral calculus aids in image enhancement, edge detection, and image reconstruction.	Image Source
		8

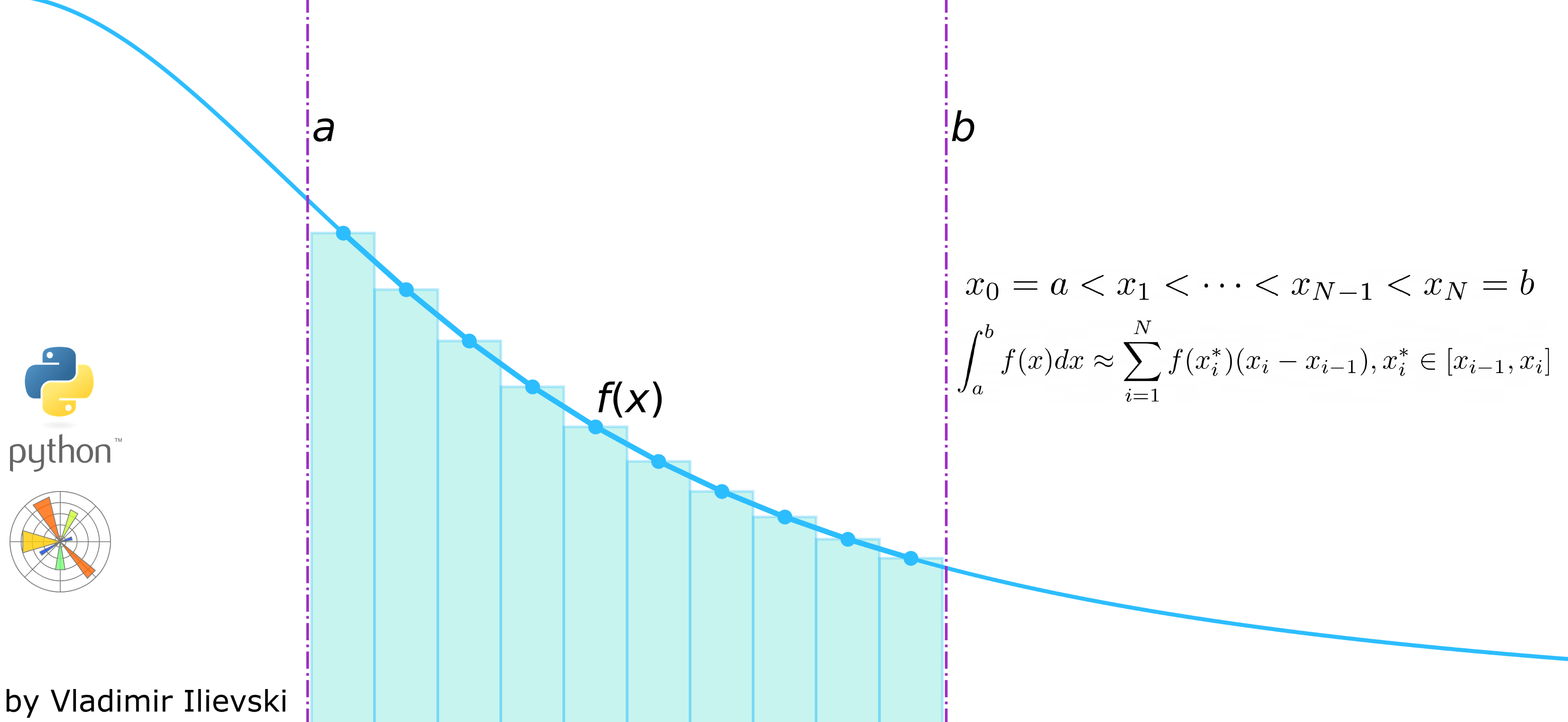
Numerical Methods
Integral calculus is used in numerical methods to approximate definite integrals. Techniques like Riemann sums and Simpson's rule are employed to numerically evaluate integrals. These methods are particularly useful when the antiderivative of a function cannot be determined analytically.	Image Source
		9

Conclusion
Integral calculus has a wide range of applications in various fields. It allows us to solve complex problems, calculate areas and volumes, analyze motion and forces, and optimize systems. Understanding the applications of integral calculus enables us to make accurate predictions and solve real-world problems.	Image Source
		10

References (download PPTX file for details)
Stewart, J. (2015). Calculus: Early Transcend... Anton, H., Bivens, I., & Davis, S. (2012). Ca... Simmons, G. F. (2011). Calculus with Analytic...
		11

Join the SlideMake Community