Application Of Vector Calculus Presentation

Introduction
Vector calculus is a branch of mathematics that deals with vector fields and their derivatives. It has a wide range of applications in physics, engineering, computer graphics, and many other fields. By studying vector calculus, we can understand the behavior of physical quantities like velocity, acceleration, electric fields, and fluid flow.	Image Source
		1

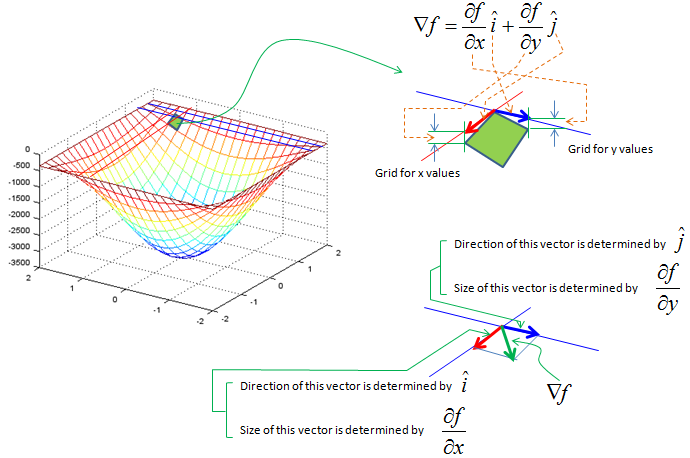
Gradient
The gradient is a fundamental concept in vector calculus. It represents the rate of change and the direction of the steepest ascent of a scalar field. The gradient is used in optimization problems, such as finding the maximum or minimum values of a function.	Image Source
		2

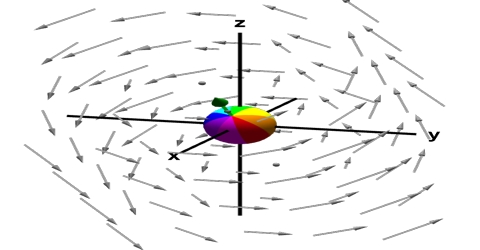
Divergence
Divergence measures the tendency of a vector field to either converge or diverge at a given point. It is used to analyze fluid flow, electric fields, and gravitational fields. Divergence helps us understand the behavior of flux and the sources or sinks of a vector field.	Image Source
		3

Curl
Curl measures the rotational behavior of a vector field. It is used to analyze fluid vortices, electromagnetic fields, and rotational motion. By studying the curl, we can understand the circulation and rotational effects of a vector field.	Image Source
		4

Line Integrals
Line integrals calculate the total effect of a vector field along a curve. They are used to calculate work done by a force, circulation of a fluid, and flux of a vector field across a curve. Line integrals help us understand the path-dependent behavior of vector fields.	Image Source
		5

Surface Integrals
Surface integrals calculate the total effect of a vector field across a surface. They are used to calculate flux through a surface, total mass flow, and electric charge enclosed by a surface. Surface integrals help us understand the behavior of vector fields in three-dimensional space.	Image Source
		6

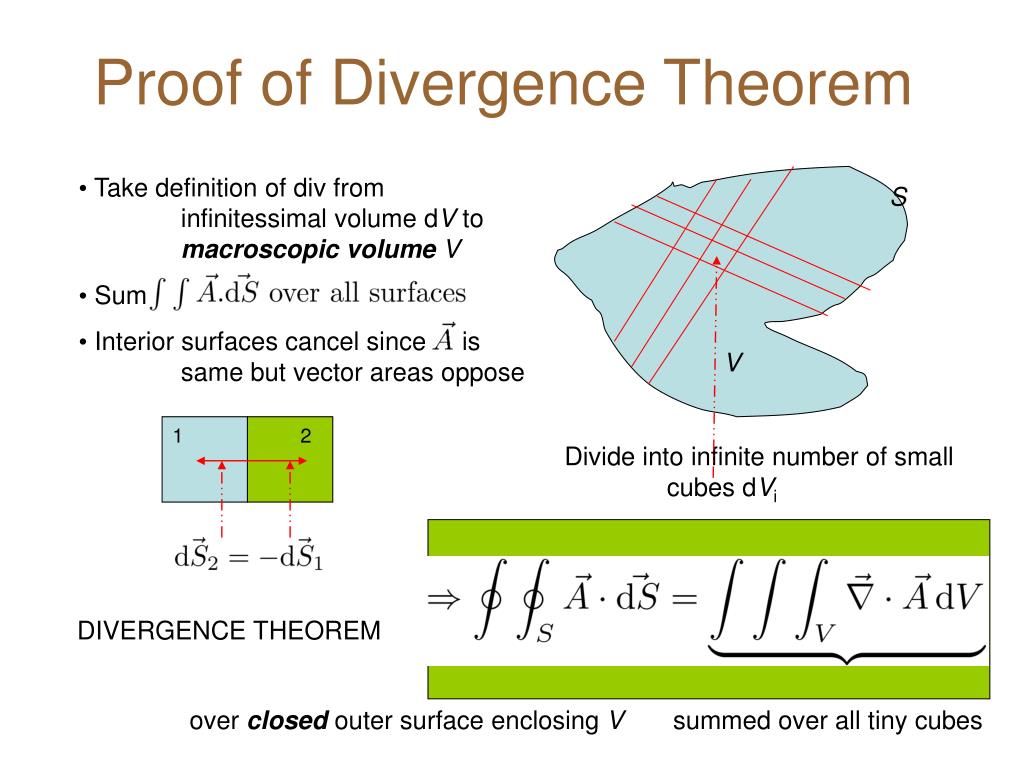
Gauss's Divergence Theorem
Gauss's Divergence Theorem relates the flux of a vector field across a closed surface to the divergence of the field within the enclosed volume. It is used to simplify the calculation of flux and to relate local behavior to global behavior of a vector field. Gauss's Divergence Theorem is a powerful tool in physics and engineering.	Image Source
		7

Stokes' Theorem
Stokes' Theorem relates the circulation of a vector field around a closed curve to the curl of the field within the enclosed surface. It is used to calculate circulation, work done in a closed loop, and to relate local rotational behavior to global rotational behavior. Stokes' Theorem is widely used in electromagnetism and fluid dynamics.	Image Source
		8

Applications in Physics
Vector calculus is extensively used in physics for studying electric fields, magnetic fields, fluid flow, and quantum mechanics. It helps us understand the behavior of particles in motion, the forces acting on them, and the distribution of physical quantities. Without vector calculus, many fundamental concepts in physics would be difficult to describe and analyze.	Image Source
		9

Applications in Engineering
Vector calculus is crucial in engineering for analyzing stress and strain in structures, fluid flow in pipes, electromagnetic fields, and signal processing. It helps engineers design efficient systems, optimize performance, and understand the behavior of physical phenomena. Vector calculus is an essential tool in various engineering disciplines, including civil, mechanical, electrical, and aerospace engineering.	Image Source
		10

Conclusion
Vector calculus is a powerful mathematical tool for analyzing and understanding vector fields in various fields, including physics and engineering. It allows us to describe the behavior of physical quantities, calculate flux, circulation, and understand the sources and sinks of vector fields. By studying vector calculus, we can solve complex problems and gain insights into the fundamental laws of nature.	Image Source
		11

Join the SlideMake Community